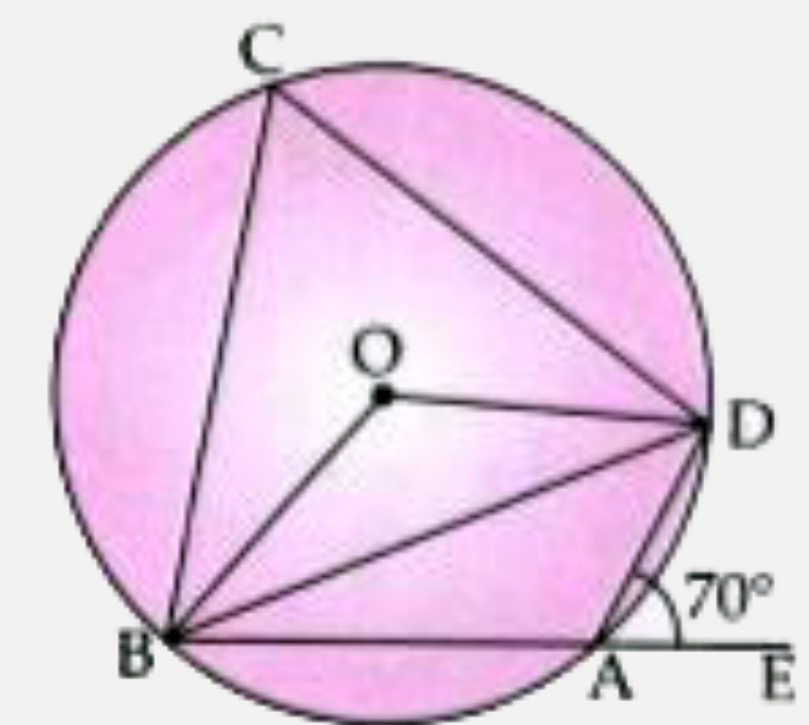
In the figure given , O is the centre of the circle . ∠DAE=70∘ , Find the giving suitable reasons , the measure of
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD
To solve the problem step by step, we will find the measures of angles BCD, BOD, and OBD based on the information provided.
Step 1: Find angle DAB
Given that angle DAE = 70 degrees, we know that angles DAB and DAE form a linear pair. Therefore, we can write:
Angle DAB+Angle DAE=180∘
Substituting the value of angle DAE:
Angle DAB+70∘=180∘
Now, solving for angle DAB:
Angle DAB=180∘−70∘=110∘
Step 2: Find angle BCD
Since angles DAB and BCD are opposite angles in a cyclic quadrilateral, we can use the property that the sum of opposite angles in a cyclic quadrilateral is 180 degrees:
Angle DAB+Angle BCD=180∘
Substituting the value of angle DAB:
110∘+Angle BCD=180∘
Now, solving for angle BCD:
Angle BCD=180∘−110∘=70∘
Step 3: Find angle BOD
Angle BOD is the angle at the center of the circle that subtends the same arc as angle BCD. The relationship between these angles is given by:
Angle BOD=2×Angle BCD
Substituting the value of angle BCD:
Angle BOD=2×70∘=140∘
Step 4: Find angle OBD
To find angle OBD, we can use the property of triangles. In triangle OBD, the sum of the angles is 180 degrees. Therefore:
Angle OBD=12(180∘−Angle BOD)
Substituting the value of angle BOD:
Angle OBD=12(180∘−140∘)=12×40∘=20∘
Summary of Angle Measures
- Angle BCD = 70 degrees
- Angle BOD = 140 degrees
- Angle OBD = 20 degrees
Given that angle DAE = 70 degrees, we know that angles DAB and DAE form a linear pair. Therefore, we can write:
Since angles DAB and BCD are opposite angles in a cyclic quadrilateral, we can use the property that the sum of opposite angles in a cyclic quadrilateral is 180 degrees:
Angle BOD is the angle at the center of the circle that subtends the same arc as angle BCD. The relationship between these angles is given by:
To find angle OBD, we can use the property of triangles. In triangle OBD, the sum of the angles is 180 degrees. Therefore:
- Angle BCD = 70 degrees
- Angle BOD = 140 degrees
- Angle OBD = 20 degrees
Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)
10 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
In the figure given, O is the centre of the circle. ∠DAE=70∘. Find, giving suitable reason, the measure of : (i) ∠BCD (ii) ∠BOD (iii) ∠OBD
View SolutionIn the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.

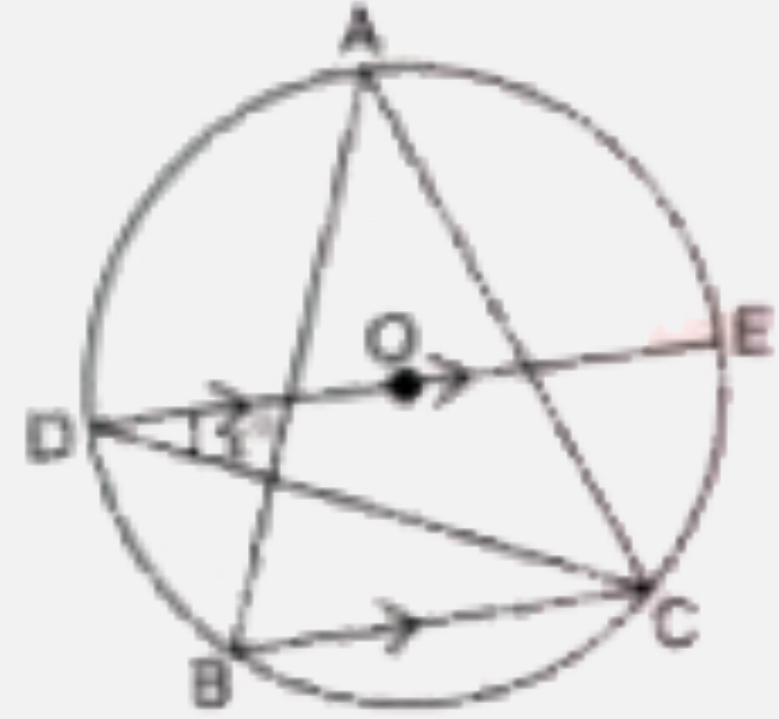
View SolutionIn the given figure BC//DE and O is the centre of the circle . If ∠CDE=x∘ , find in terms of x∘ the value of ∠BAC.
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=70∘, then find the value of ∠OCD.

View SolutionIn the adjoining figure, O is the centre of circle. If ∠DAB=50∘ find the values of x and y.

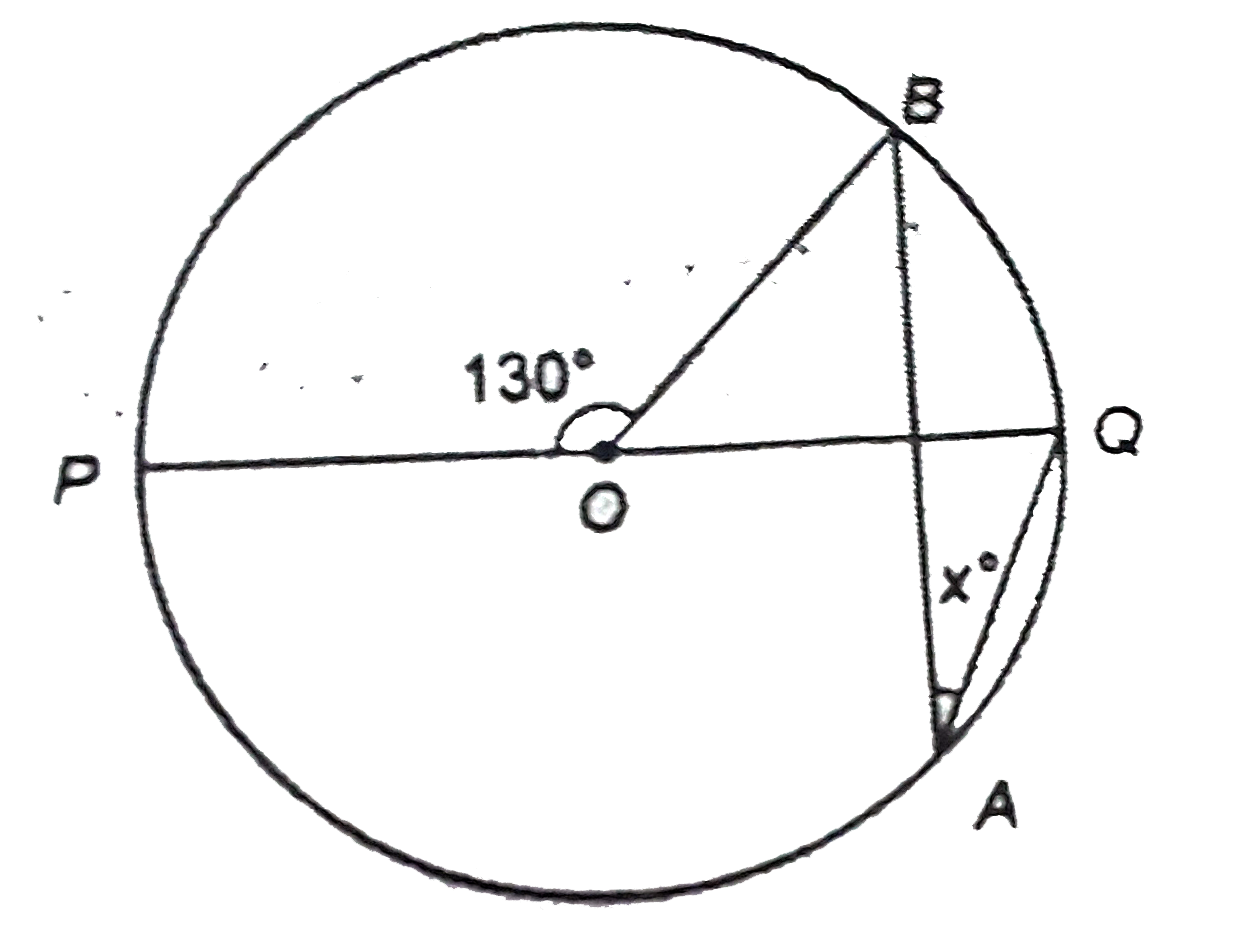
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠BOP=130∘, then find the value of x.
View SolutionIn the given figure, O is the centre of a circle and ∠ADC=130∘.If ∠BAC=x∘, Find the value of x.

View SolutionIn the given 'O' is the centre of the circle, Arc AB=ArcBC=Cd.If∠OAB=48∘, find:
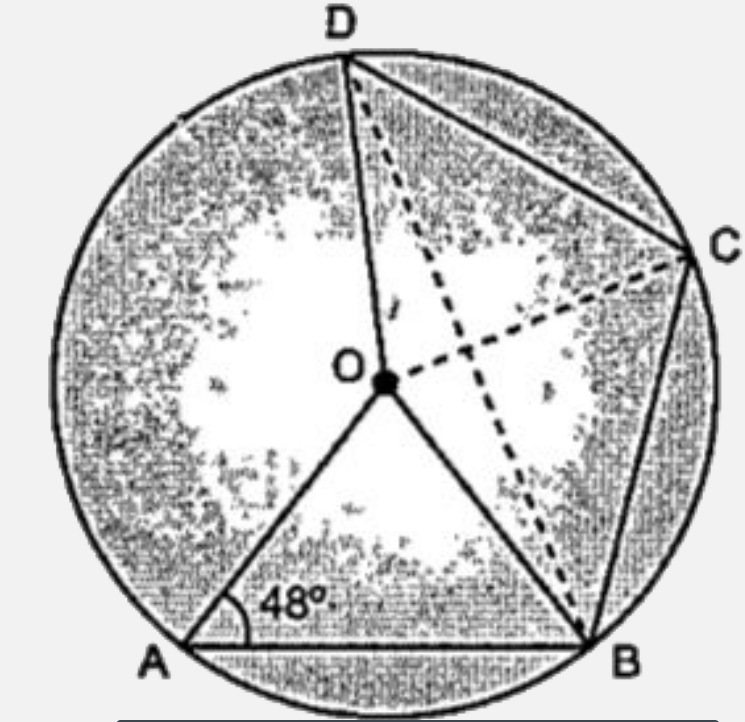
∠OBD
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
View SolutionIn the adjoining , O is the centre of the circle. ACB is a segment. If ∠OAB=30∘, then find the value of ∠ACB.
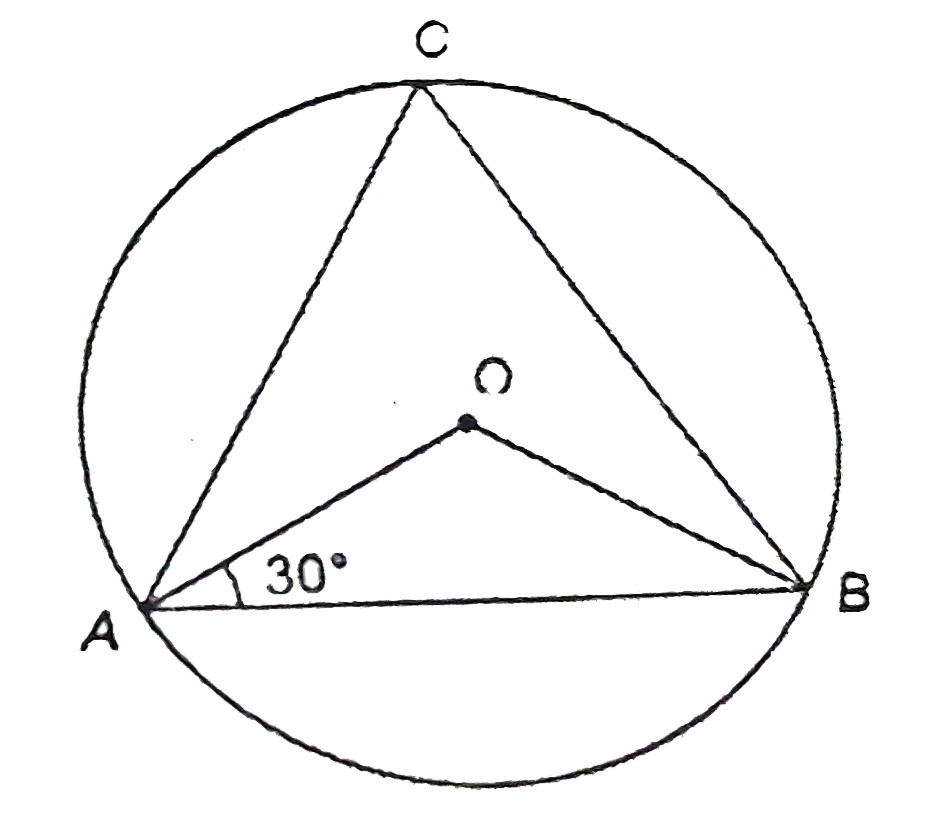
View Solution
