A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3-5 m. Calculate :
the internal volume of the container in m?.
The correct Answer is:359.33cm3
To find the internal volume of the metal container, which consists of a cylinder surmounted by a hemisphere, we will follow these steps:
Step 1: Identify the dimensions
- The internal radius r of the cylinder (and hemisphere) is given as 3.5m.
- The internal height h of the cylinder is given as 7m.
Step 2: Calculate the volume of the cylinder
The formula for the volume Vc of a cylinder is:
Vc=πr2h
Substituting the values:
Vc=π(3.5)2(7)
Calculating (3.5)2:
(3.5)2=12.25
Now substituting back:
Vc=π(12.25)(7)=85.75π
Step 3: Calculate the volume of the hemisphere
The formula for the volume Vh of a hemisphere is:
Vh=23πr3
Substituting the radius:
Vh=23π(3.5)3
Calculating (3.5)3:
(3.5)3=42.875
Now substituting back:
Vh=23π(42.875)=85.753π
Step 4: Calculate the total volume of the container
The total volume V of the container is the sum of the volumes of the cylinder and the hemisphere:
V=Vc+Vh
Substituting the values:
V=85.75π+85.753π
To combine these, we can find a common denominator:
V=257.253π+85.753π=3433π
Step 5: Substitute the value of π
Using π≈227:
V=3433×227
Calculating this:
V=343×223×7=756621
Calculating 756621:
V≈359.33m3
Final Answer
The internal volume of the container is approximately 359.33m3.
---
- The internal radius r of the cylinder (and hemisphere) is given as 3.5m.
- The internal height h of the cylinder is given as 7m.
The formula for the volume Vc of a cylinder is:
Vc=πr2h
Substituting the values:
Vc=π(3.5)2(7)
Calculating (3.5)2:
(3.5)2=12.25
Now substituting back:
Vc=π(12.25)(7)=85.75π
The formula for the volume Vh of a hemisphere is:
Vh=23πr3
Substituting the radius:
Vh=23π(3.5)3
Calculating (3.5)3:
(3.5)3=42.875
Now substituting back:
Vh=23π(42.875)=85.753π
The total volume V of the container is the sum of the volumes of the cylinder and the hemisphere:
V=Vc+Vh
Substituting the values:
V=85.75π+85.753π
To combine these, we can find a common denominator:
V=257.253π+85.753π=3433π
Using π≈227:
V=3433×227
Calculating this:
V=343×223×7=756621
Calculating 756621:
V≈359.33m3
The internal volume of the container is approximately 359.33m3.
Topper's Solved these Questions
Similar Questions
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3-5 m. Calculate :
the total area of the internal surface, excluding the base,View SolutionA vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylinder is 143 m and the diameter of hemisphere is 3.5 m. Calculate the volume and the internal surface area of the solid.
View SolutionThe adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other end. Given that common radius =3.5 cm the height of the cylinder =6.5 cm and the total height =12.8 cm , claculate the volume of the solid correct to the nearest cm.
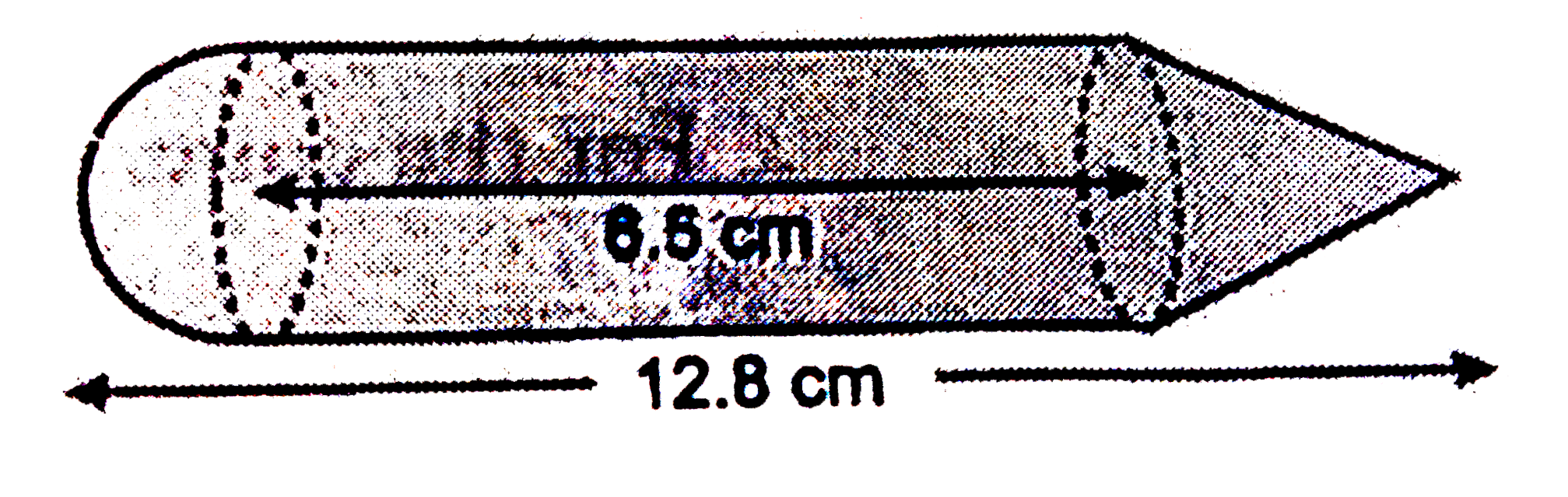 View Solution
View SolutionA boiler is in the form of a cylinder 2 m long with hemispherical ends each of 2 metre diameter. Find the volume of the boiler.
View SolutionA solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
View SolutionMayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath.
View SolutionMayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath.
View SolutionThe radius and height of a cylinder are equal. If the radius of the sphere is equal to the height of the cylinder, then the ratio of the rates of increase of the volume of the sphere and the volume of the cylinder, is
View SolutionA metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
View SolutionA metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
View Solution

