The given figure shows, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that:
AB2=AC×AP
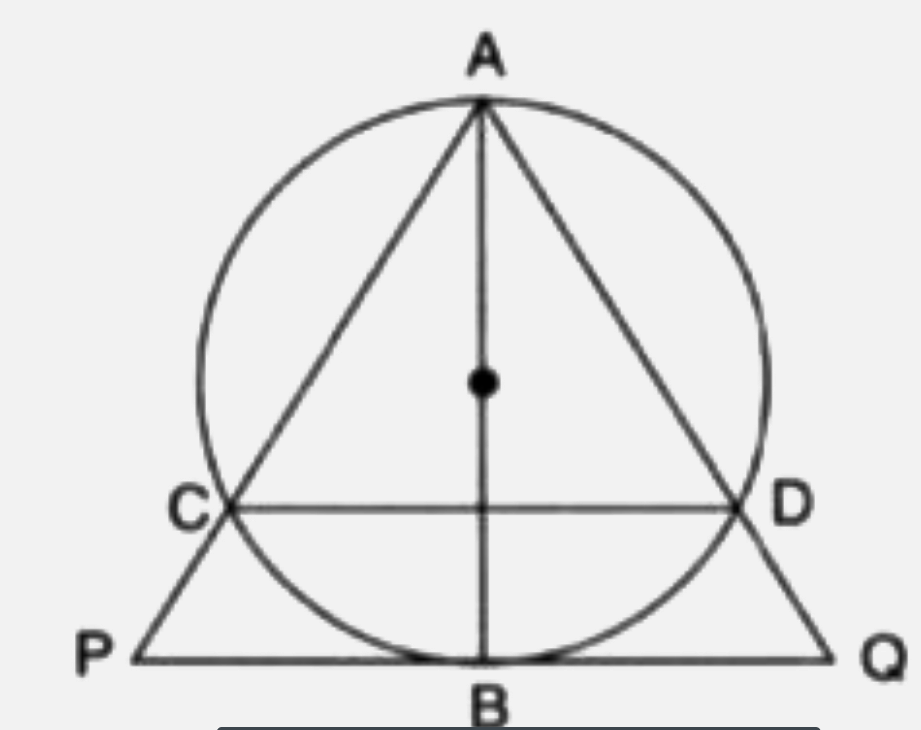
Step by step video & image solution for The given figure shows, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that: AB^2 = AC xxAP by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MIXED PRACTICE BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B
52 Videos
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (E)
23 Videos
- PROBABILITYBOOK - ICSECHAPTER - PROBABILITYEXERCISE - EXERCISE 25(C)
106 Videos
Similar Questions
AB is the diameter of a circle with centre O. A line PQ touches the given circle at point R and cuts the tangents to the circle through A and B at points P and Q respectively. Prove that ∠POQ=90∘
View SolutionIn Figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionIn ΔABC,AB=AC and the bisectors of ∠B and ∠C meet AC and AB at point D and E respectively. Prove that BD=CE.
View SolutionProve that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
View SolutionIf AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
View SolutionIn the given figure the sides AB, BE and CA of triangle ABC touch a circle with centre O and radius r at P,Q and R respectively.
Prove that : (i)AB+CQ=AC+BQ

View SolutionThe given figure shows an isosceles triangle ABC inscribed in a circle such that AB=AC. If DAE is a tangent to the circle at point A, prove that DE is parallel to BC.
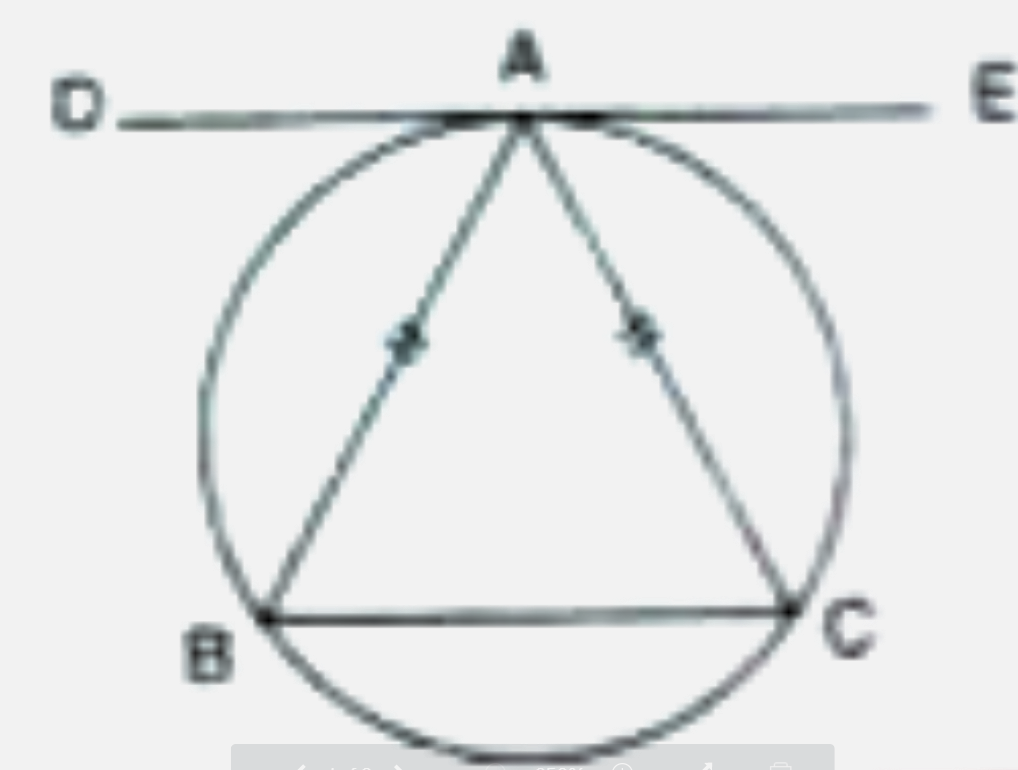
View SolutionIn the given figure, O is the centre of the circle. If chord AB= chord AC, OP⊥ABandOQ⊥AC, show that: PB= QC

View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View Solution
