AB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
To solve the problem step by step, we will analyze the given information and apply the properties of circles and triangles.
Step 1: Understand the Geometry
We have a circle with diameter AB. Since AB is a diameter, the center of the circle (O) is the midpoint of AB. We also know that CD is a chord parallel to AB, and that 2CD=AB.
Step 2: Define the Lengths
Let the length of AB (the diameter) be d. Therefore, AB=d and since 2CD=AB, we have:
CD=d2
Step 3: Identify the Tangent and Chord
The tangent at point B meets the line AC produced at point E. We need to find the length AE.
Step 4: Use Triangle Properties
Since AB is a diameter, triangle ABE is a right triangle (by the Inscribed Angle Theorem). Thus, angle ABE = 90 degrees.
Step 5: Apply the Cosine Rule
In triangle ABE, we can apply the cosine rule. We know:
- AB=d
- Angle ABE = 90 degrees
- Let AE = x (the length we want to find)
Using the cosine of angle CAB (which is 60 degrees as stated in the video), we apply:
cos(60∘)=ABAE
Substituting the known values:
12=dx
Step 6: Solve for AE
Rearranging the equation gives:
x=2d
Step 7: Conclusion
Since we defined d as the length of the diameter AB, we conclude:
AE=2×AB
Final Answer
Thus, the length of AE is:
AE=2×d
We have a circle with diameter AB. Since AB is a diameter, the center of the circle (O) is the midpoint of AB. We also know that CD is a chord parallel to AB, and that 2CD=AB.
Let the length of AB (the diameter) be d. Therefore, AB=d and since 2CD=AB, we have:
CD=d2
The tangent at point B meets the line AC produced at point E. We need to find the length AE.
Since AB is a diameter, triangle ABE is a right triangle (by the Inscribed Angle Theorem). Thus, angle ABE = 90 degrees.
In triangle ABE, we can apply the cosine rule. We know:
- AB=d
- Angle ABE = 90 degrees
- Let AE = x (the length we want to find)
cos(60∘)=ABAE
Substituting the known values:
12=dx
Rearranging the equation gives:
x=2d
Since we defined d as the length of the diameter AB, we conclude:
AE=2×AB
Thus, the length of AE is:
AE=2×d
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:CENGAGE ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:All Questions
Explore 886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGE ENGLISHChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Multiple correct answers type
Explore 11 Videos
Similar Questions
AB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionProve that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
View SolutionAD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionIn Figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘
View SolutionIn the given figure AB is the diameter and AC is the chord of a circle such that ∠BAC=30∘. The tangent at C intersects AB produced at D. Prove that :BC=BD.
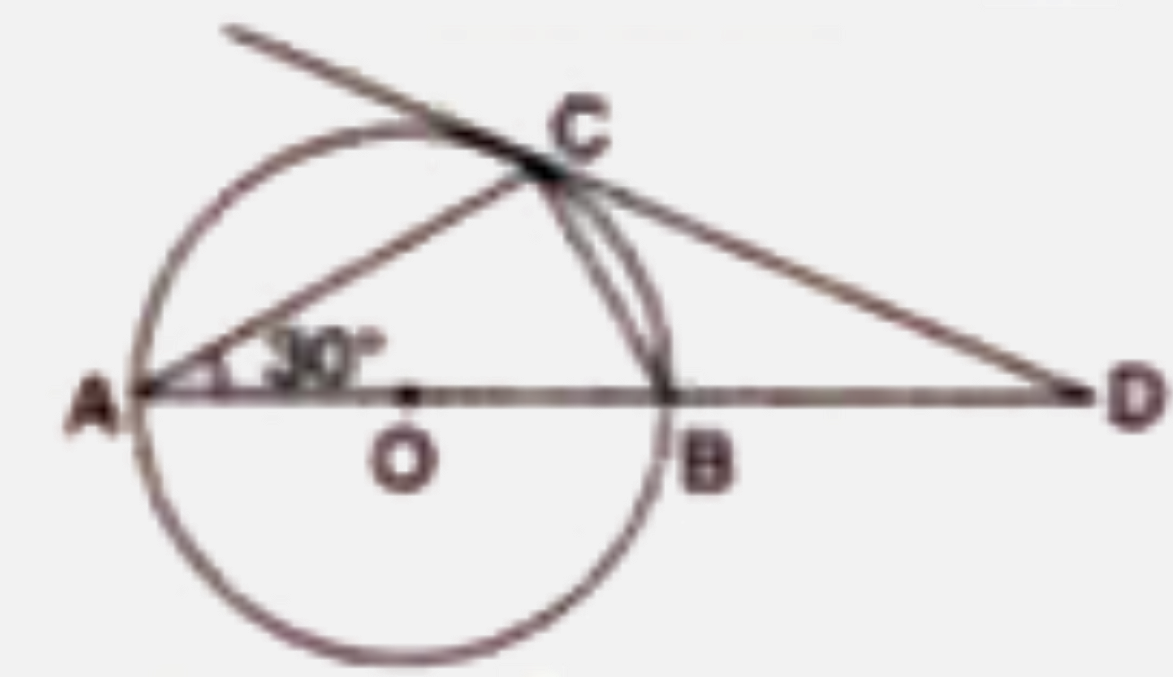
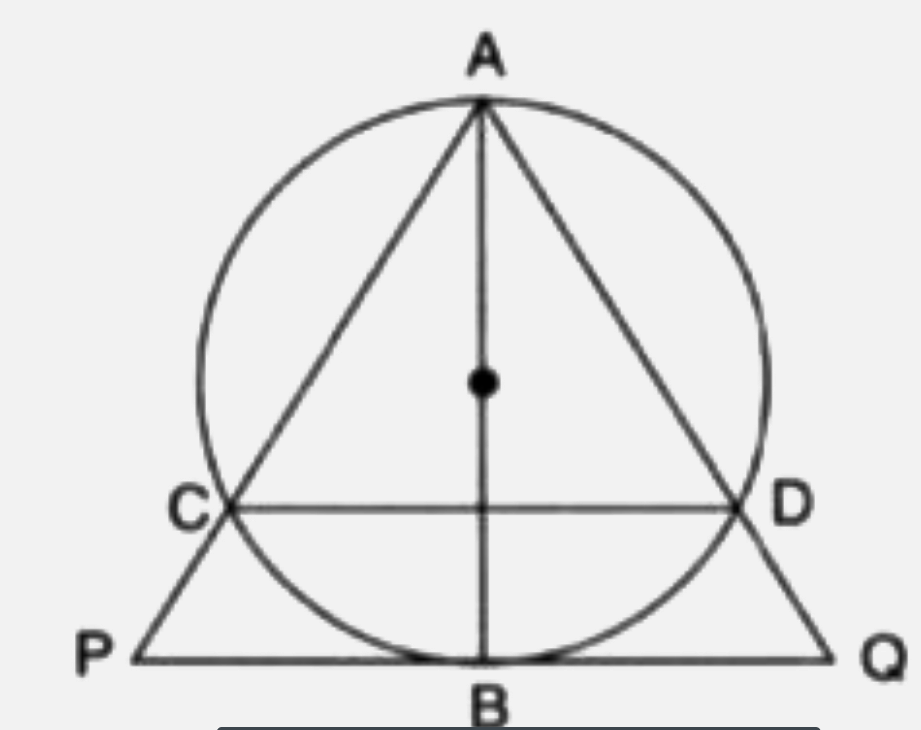
View SolutionThe given figure shows, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that:
AB2=AC×AP
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View SolutionA straight line AB is divided at C so that AC=3CB. Circles are described on ACandCB as diameters and a common tangent meets AB produced at D. Show that BD is equal to the radius of the smaller circle.
View Solution