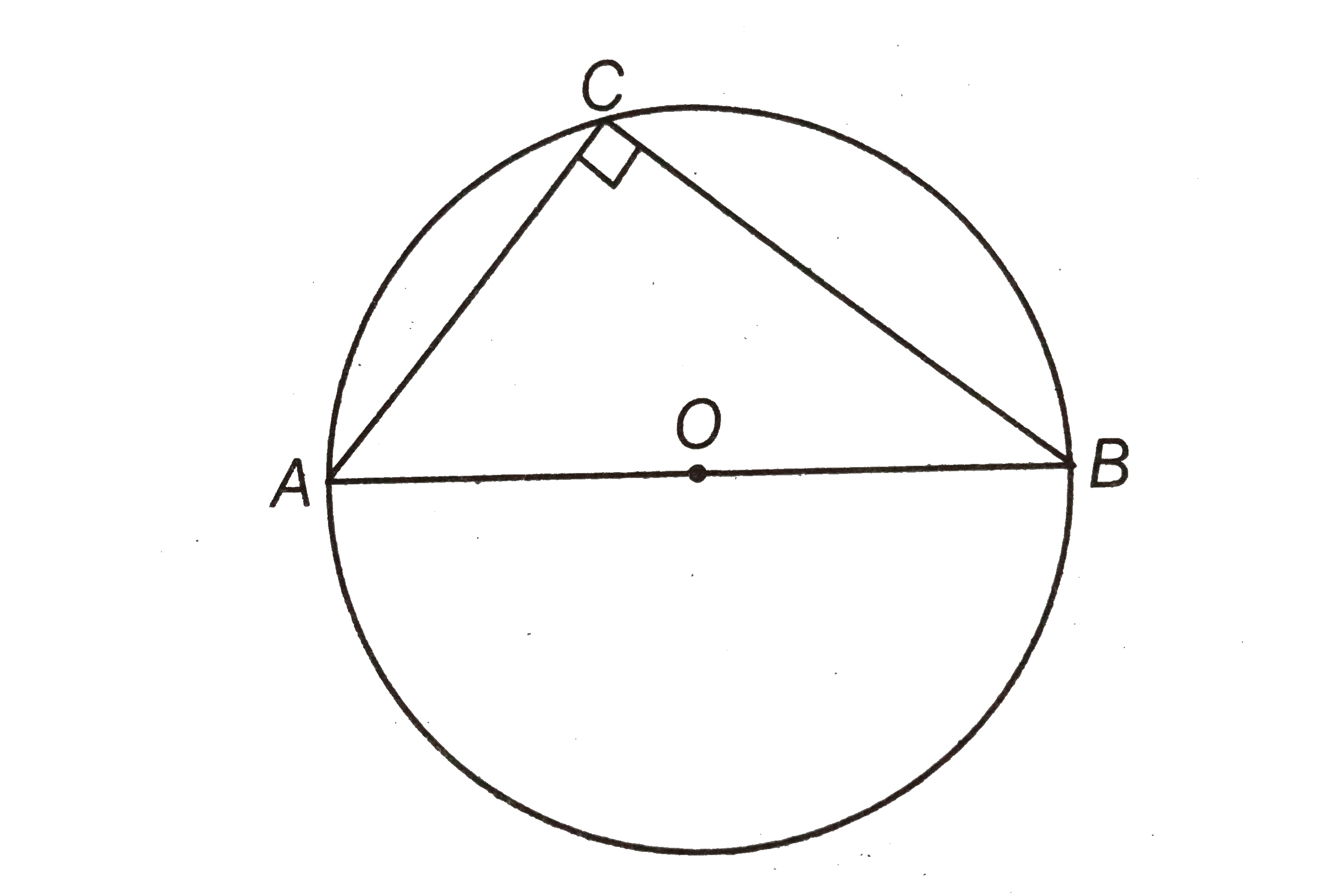
If AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
The correct Answer is:1
Since, any diameter of the circle subtends a right angle to any point on the circle.
If AOB is a diameter of a circle and C is a point on the circle, then ΔACB is right angled atC.
In right angled ΔACB, [use Pythagoras theorem]
AC2+BC2=AB2
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.3
20 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
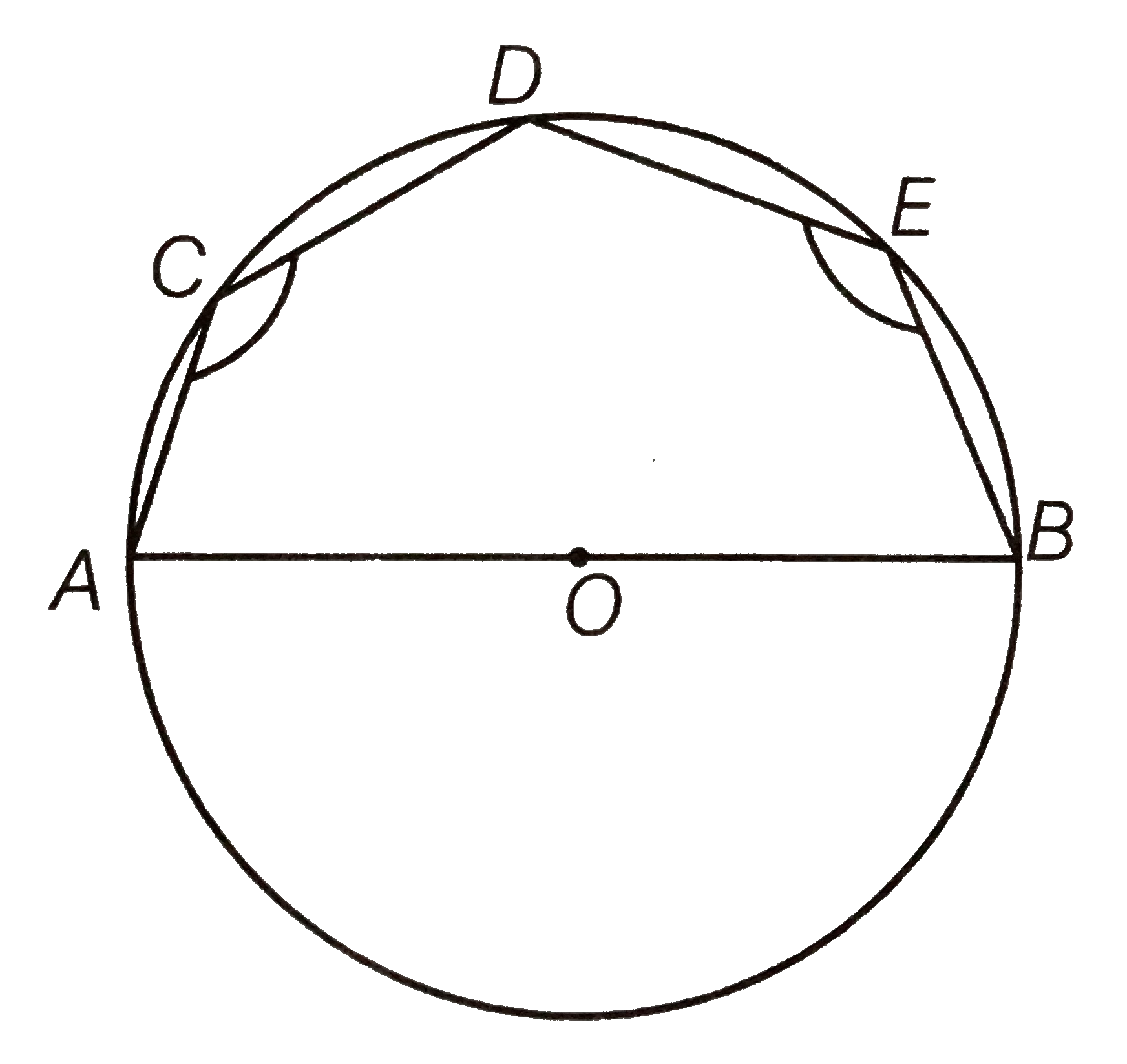
In figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD+∠BED.
View SolutionIf AOB is a diameter of the circle and AC=BC, then ∠CAB is equal to
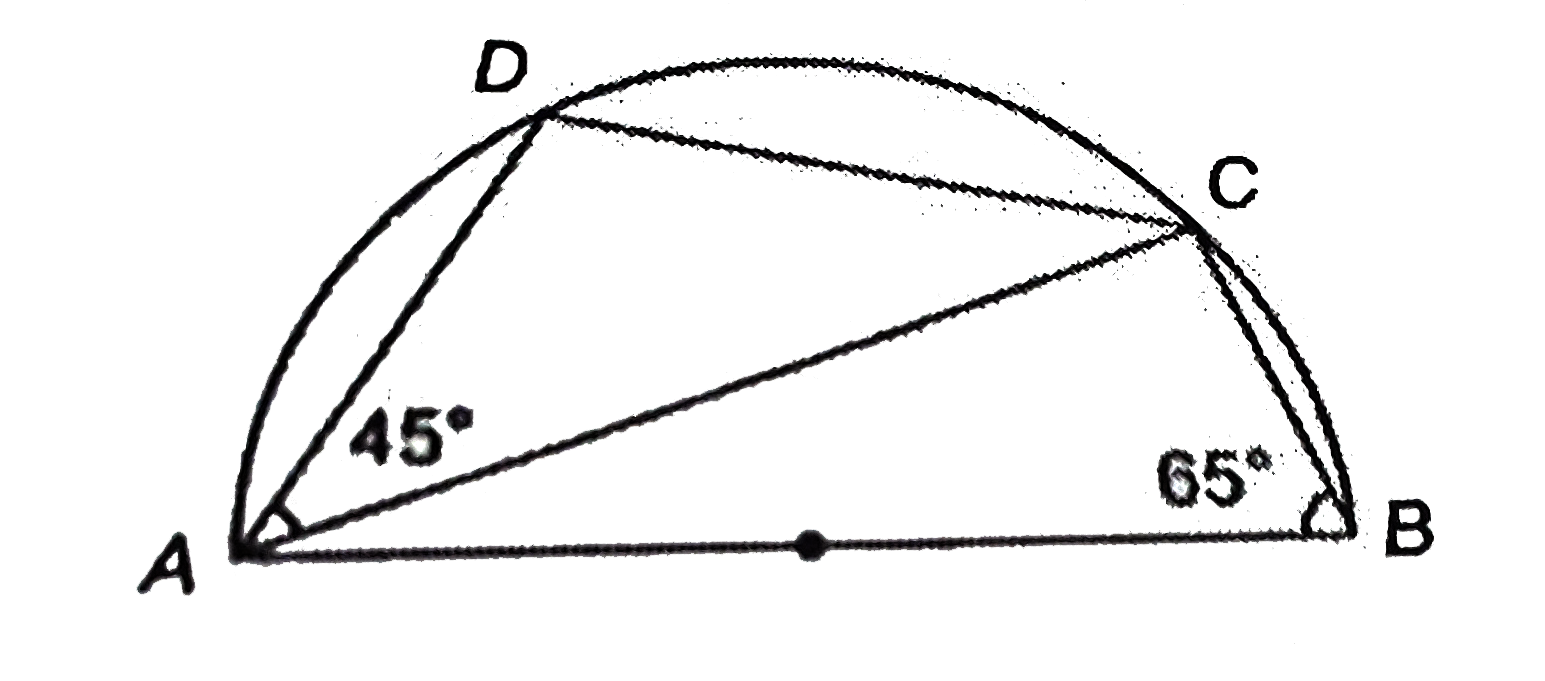
View SolutionIn the adjoining figure, AB is the diameter of the circle and two points C and D are on the circle. If ∠CAD=45∘ and ∠ABC=65∘, then find the value of ∠DCA.
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionThe given figure shows, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that:
AB2=AC×AP
View SolutionA chord of the circle x2+y2=a2 cuts it at two points A and B such that ∠AOB=π/2, where O is the centre of the circle. If there is a moving point P on this circle, then the locus of the orthocentre of ΔPAB will be a
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
View SolutionThe diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure (Fig 11.12) AB is a diameter of the circle; C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).
View Solution
