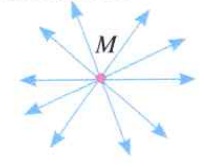
In the figure alongside. Point M is called both the point of intersection and the point of concurrence.
The correct Answer is:True
Step by step video & image solution for In the figure alongside. Point M is called both the point of intersection and the point of concurrence. by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In the figure below, line m is perpendicular to line n, and both lines intersect line q at the same point. The measure of ∠1 is (3x−10)∘, and the measure of ∠2 is (2x+10)∘. What is the measure of ∠3?
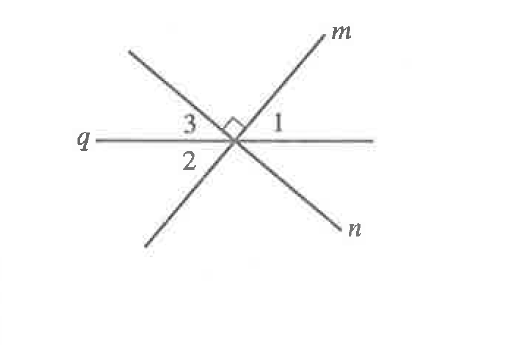 A36∘B40∘C44∘D45∘
A36∘B40∘C44∘D45∘
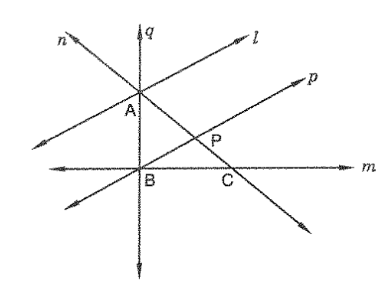
From the adjoining figure , write?
(i) Collinear points
(ii) Concurrent lines and their point of concurrence.
View SolutionAssertion: Number of triangles formed by n concurrent lines and a line which is parallel to one of the n concurrent lines is n−1C2. Reason: One and only one triangle is formed by three lines out of which 2 are concurrent and third line is not passing through the point of intersection of the concurrent lines and not parallel to any of the concurrent lines. (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not the correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
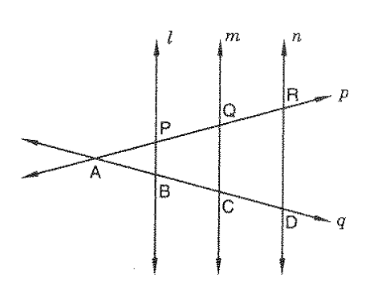
View SolutionFrom Figure, name
(i)All pairs of parallel lines.
(ii)all pairs of intersecting lines.
(iii)ines of whose point of intersection in P
(iv)lines whose point of intersection in C
(v)lines whose point of intersection in R
(vi)Collinear points.
View SolutionThe point of intersection of the asymptotes with the directrices lie on
View SolutionFind the maximum number of points of intersection of 6 circles.
View SolutionProve that the medians of a triangle are concurrent and find the position vector of the point of concurrency (that is, the centroid of the triangle)
View SolutionShow, by vector methods, that the angularbisectors of a triangle are concurrent and find an expression for the position vector of the point of concurrency in terms of the position vectors of the vertices.
View Solution