Assertion: Number of triangles formed by n concurrent lines and a line which is parallel to one of the n concurrent lines is n−1C2. Reason: One and only one triangle is formed by three lines out of which 2 are concurrent and third line is not passing through the point of intersection of the concurrent lines and not parallel to any of the concurrent lines. (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not the correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
To solve the question, we need to analyze both the assertion and the reason provided.
Step 1: Understanding the Assertion
The assertion states that the number of triangles formed by n concurrent lines and a line which is parallel to one of the n concurrent lines is given by (n−12).
- Concurrent Lines: Lines that intersect at a single point.
- Triangles Formation: A triangle can be formed by selecting two concurrent lines and one line that is not concurrent with them.
Step 2: Analyzing the Reason
The reason states that one and only one triangle is formed by three lines, where two are concurrent and the third line is neither passing through the point of intersection of the concurrent lines nor parallel to any of the concurrent lines.
- For a triangle to be formed, we need:
- Two lines that are concurrent (which will intersect at a point).
- A third line that is not concurrent and does not pass through the intersection point.
Step 3: Finding the Number of Triangles
To find the number of triangles formed:
1. We have n concurrent lines.
2. To form a triangle, we can choose any two lines from these n concurrent lines. The number of ways to choose 2 lines from n lines is given by (n2).
3. However, since we need a third line that is parallel to one of the n lines, we can only choose from n−1 lines (excluding the one that is parallel).
4. Therefore, the number of triangles formed is (n−12).
Conclusion
Both the assertion and the reason are true, and the reason correctly explains the assertion.
Final Answer
The correct option is (A) Both A and R are true and R is the correct explanation of A.
---
The assertion states that the number of triangles formed by n concurrent lines and a line which is parallel to one of the n concurrent lines is given by (n−12).
- Triangles Formation: A triangle can be formed by selecting two concurrent lines and one line that is not concurrent with them.
The reason states that one and only one triangle is formed by three lines, where two are concurrent and the third line is neither passing through the point of intersection of the concurrent lines nor parallel to any of the concurrent lines.
- Two lines that are concurrent (which will intersect at a point).
- A third line that is not concurrent and does not pass through the intersection point.
To find the number of triangles formed:
1. We have n concurrent lines.
2. To form a triangle, we can choose any two lines from these n concurrent lines. The number of ways to choose 2 lines from n lines is given by (n2).
3. However, since we need a third line that is parallel to one of the n lines, we can only choose from n−1 lines (excluding the one that is parallel).
4. Therefore, the number of triangles formed is (n−12).
Both the assertion and the reason are true, and the reason correctly explains the assertion.
The correct option is (A) Both A and R are true and R is the correct explanation of A.
Similar Questions
Assertion: If m parallel lines are intersected by n other parallel llines, then the number of parallelograms thus formed is mn(m−1)(n−1)4, Reason: A selection of 4 lines 2 from m parallel lines and 2 from n parallel lines gives one parallelogram. (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not the correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
View SolutionAssertion: If each of m points on one straight line be joined to each of n points on the other straight line terminated by the points, then number of points of intersection of these lines excluding the points on the given lines is mn(m−1)(n−1)2 Reason: Two points on one line and two points on other line gives one such point of intersection. (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not the correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
View SolutionProve that the medians of a triangle are concurrent.
View SolutionIn the figure alongside. Point M is called both the point of intersection and the point of concurrence.
View SolutionFrom Fig., write concurrent lines and their points of concurrence.
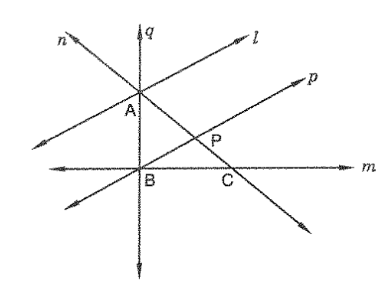
View SolutionDefine the following terms: Concurrent lines
View SolutionProve that the altitudes of a triangle are concurrent.
View SolutionLimes p,q and r are concurrent . Lines q,r and s are also concurrent . Will all the four lines p,q,r and s be concurrent ?
View SolutionShow that the altitudes of a triangle are concurrent
View SolutionIf there are nine straight lines of which five are concurrent at a point and the other four are concurrent at another point and no two of these nine lines are parallel, then the number of points of intersection is equal to
View Solution
