A rigid rod that can move freely around a fixed point of support
Step-by-Step Text Solution:
1. Understanding the Definition: A rigid rod that can move freely around a fixed point of support refers to a lever.
2. Identifying Components:
- Lever: The rigid rod itself.
- Fulcrum: The fixed point around which the lever rotates.
- Effort: The force applied to the lever to move the load.
- Load: The object that is being moved or lifted by the lever.
3. Function of a Lever: A lever is a type of simple machine that helps in lifting or moving heavy objects with less effort.
4. Types of Levers: Levers can be classified into three types based on the position of the fulcrum, effort, and load:
- First-Class Lever: Fulcrum is between the effort and the load (e.g., seesaw).
- Second-Class Lever: Load is between the fulcrum and the effort (e.g., wheelbarrow).
- Third-Class Lever: Effort is between the fulcrum and the load (e.g., tweezers).
5. Conclusion: A rigid rod that can move freely around a fixed point of support is indeed a lever, which is an essential tool in physics and mechanics.
- Lever: The rigid rod itself.
- Fulcrum: The fixed point around which the lever rotates.
- Effort: The force applied to the lever to move the load.
- Load: The object that is being moved or lifted by the lever.
- First-Class Lever: Fulcrum is between the effort and the load (e.g., seesaw).
- Second-Class Lever: Load is between the fulcrum and the effort (e.g., wheelbarrow).
- Third-Class Lever: Effort is between the fulcrum and the load (e.g., tweezers).
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MODEL TEST PAPERS EXERCISE - TEST PAPER II (SECTION I) Choose the correct option4videos
MODEL TEST PAPERS
- BOOK - ICSECHAPTER - MODEL TEST PAPERS EXERCISE - TEST PAPER II (SECTION I) Write T for True and F for False . Correct the False statements4videos
MODEL TEST PAPERS
- BOOK - ICSECHAPTER - MODEL TEST PAPERS EXERCISE - TEST PAPER I (SECTION II) Numerical questions3videos
MODEL TEST PAPERS
- BOOK - ICSECHAPTER - MATTEREXERCISE - Picture Based Questions2videos
MATTER
- BOOK - ICSECHAPTER - PHYSICAL QUANTITIES AND MEASUREMENT EXERCISE - Picture-Based Questions1videos
PHYSICAL QUANTITIES AND MEASUREMENT
Similar Questions
A spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
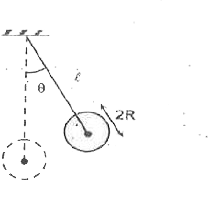View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).
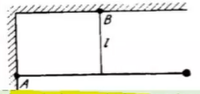
The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.View SolutionA rod of mass m can move vertically on two fixed inclined rod in vertical plane, weight of the rod is blanced by thin liquid film between rods as shown. (Surface tension of liquid is S).
If rod is displaced a little in downward direction and released, then what will be the time period of oscillation of rod.
View SolutionA weightless rigid rod AB of length / connects two equal masses m one particle is fixed at the end B and the other at the middle ofthe rod as shown in the figure-5.131. The rod can rotate in the vertical plane freely around the hinge point/4. Choose the correct option(s)
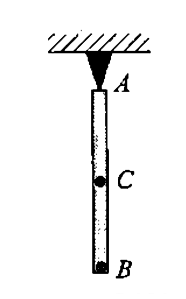
A. The minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circle is √24gl5
B. The minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circle is √24glg
C. The ratio of compressive force in the rods AC and BC is 2:1 when the masses are at highest point.
D. The ratio of compressive force in the rods AC and BC is 3:1 when the masses are at highest point.View SolutionA heavy uniform rod is hanging vertically from a fixed support. It is stretched by its own weight. The diameter of the rod is
View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
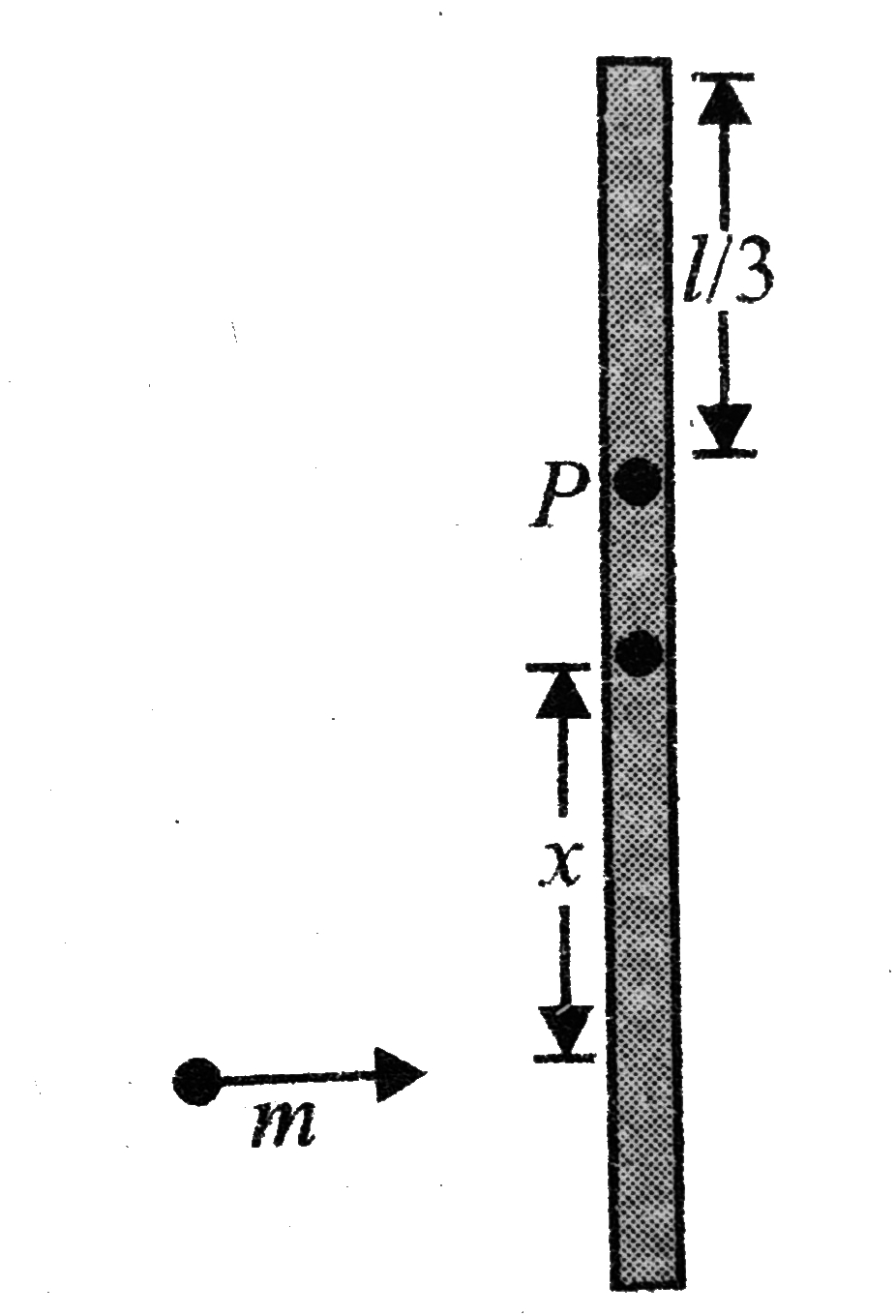View Solution
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20cm, fixed at its midpoint. The bob is displaced slightly perpenducular to the plane of the rod and string. Find period of small oscillations of the system in the form πX10s and fill the value of X.View Solution-
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20cm, fixed at its midpoint. The bob is displaced slightly perpenducular to the plane of the rod and string. Find period of small oscillations of the system in the form πX10s and fill the value of X.View Solution A rod of mass 'm and length L is attached to a L shaped plank at 'A'. rod can move freely about A. A string is tied between rod and plank as shown in figure. Whole system is moving with a constant acceleration g in x-direction
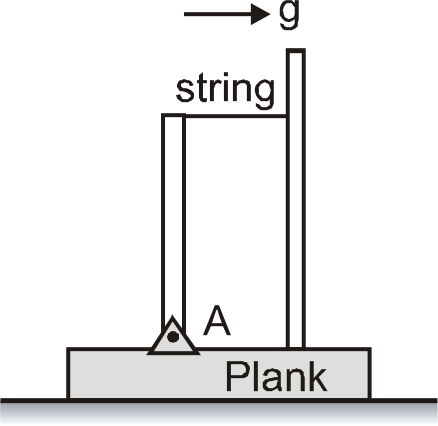
Force exerted by hinge on the rod isView SolutionA smooth rod OP is fixed vertically. A disc of mass m and radius R is rolling without slipping at the given instant on a rough horizontal surface as shown. Velocity of centre of mass C of disc is v0. A rod AB of length L is connected with disc at A, R/2 distance vertically up from centre of disc with pin joint (about which it can rotate freely), other end of the rod is attached to a small smooth ring B, which can move freely over rod OP. At an instant rod AB makes an angle 60∘ with the vertical. The velocity of ring on the vertical rod at this instant is.
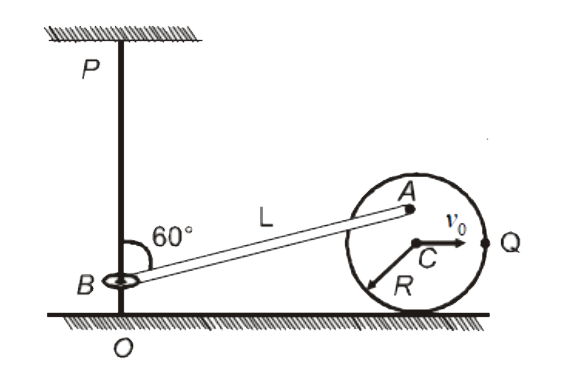View Solution