A weightless rigid rod AB of length / connects two equal masses m one particle is fixed at the end B and the other at the middle ofthe rod as shown in the figure-5.131. The rod can rotate in the vertical plane freely around the hinge point/4. Choose the correct option(s)
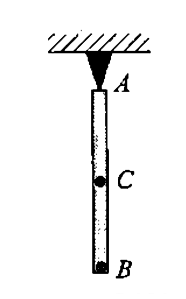
A. The minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circle is √24gl5
B. The minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circle is √24glg
C. The ratio of compressive force in the rods AC and BC is 2:1 when the masses are at highest point.
D. The ratio of compressive force in the rods AC and BC is 3:1 when the masses are at highest point.
The minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circle is √24gl5
The minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circle is √24glg
The ratio of compressive force in the rods AC and BC is 2:1 when the masses are at highest point.
The ratio of compressive force in the rods AC and BC is 3:1 when the masses are at highest point.
The correct Answer is:A, C
Step by step video & image solution for A weightless rigid rod AB of length / connects two equal masses m one particle is fixed at the end B and the other at the middle ofthe rod as shown in the figure-5.131. The rod can rotate in the vertical plane freely around the hinge point/4. Choose the correct option(s) <BR><BR>A. The minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circle is sqrt((24 gl)/(5))<BR>B. The minimum horizontal velocity required to be given to the particle B so as to make the rod go around in the complete vertical circle is sqrt((24 gl)/(g))<BR>C. The ratio of compressive force in the rods AC and BC is 2:1 when the masses are at highest point.<BR>D. The ratio of compressive force in the rods AC and BC is 3:1 when the masses are at highest point. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A weightless rod of length l carries two equal masses m one fixed at the end and other in the middle ofhte rod. The rod can revolve in a vertical plane about A. Then, horizontal velocity which must be imparted to end C of rod to deflect it to horizontal position is

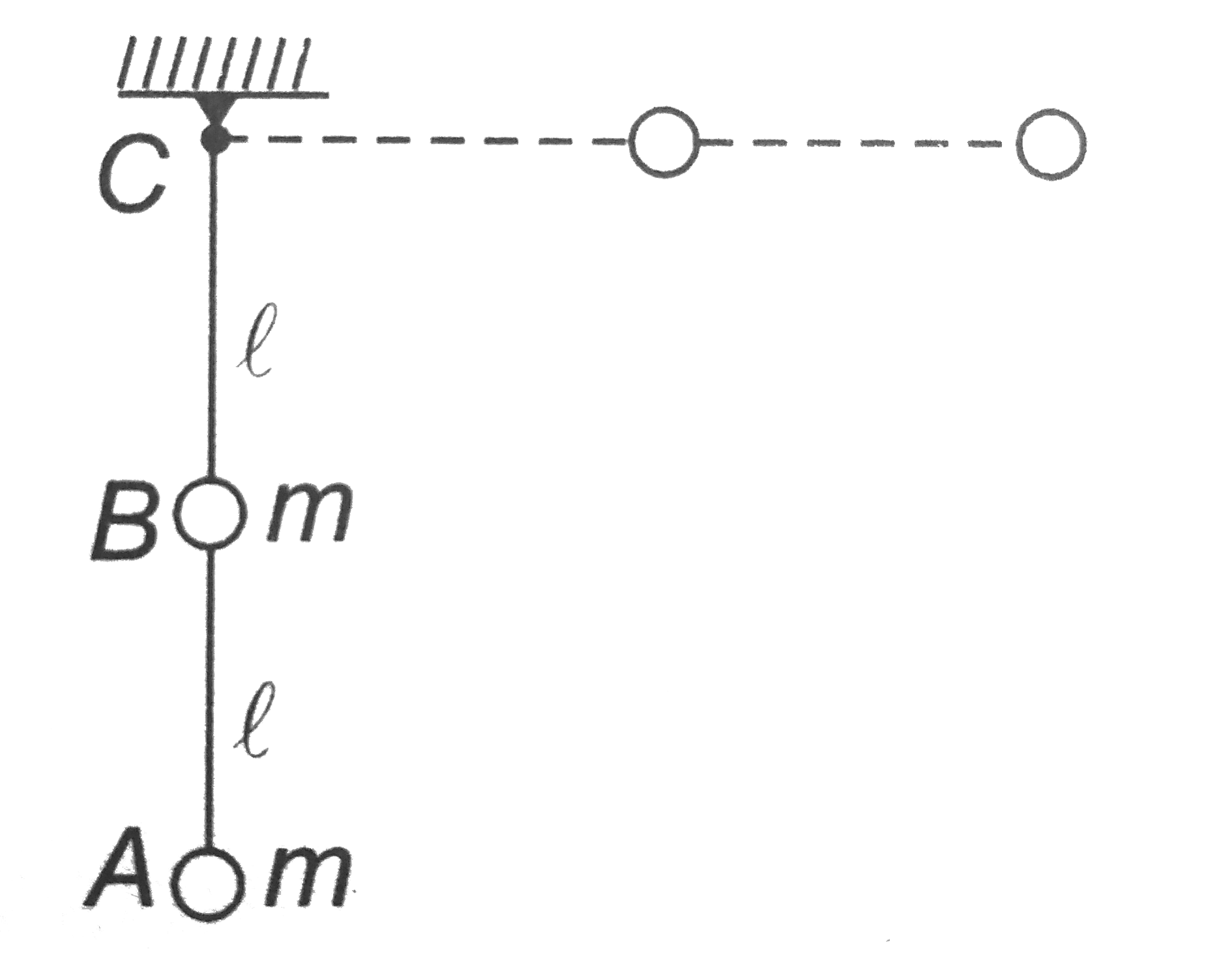
View SolutionA weightless rod of length 2l carries two equal masses 'm', one tied at lower end A and the other at the middle of the rod at B. The rod can rotate in vertical plane about a fixed horizontal axis passing thriugh C . The rod of is released from rest in horizontal possion. The speed of the mass B at the instant rod become vertical is:
View SolutionA rigid rod that can move freely around a fixed point of support
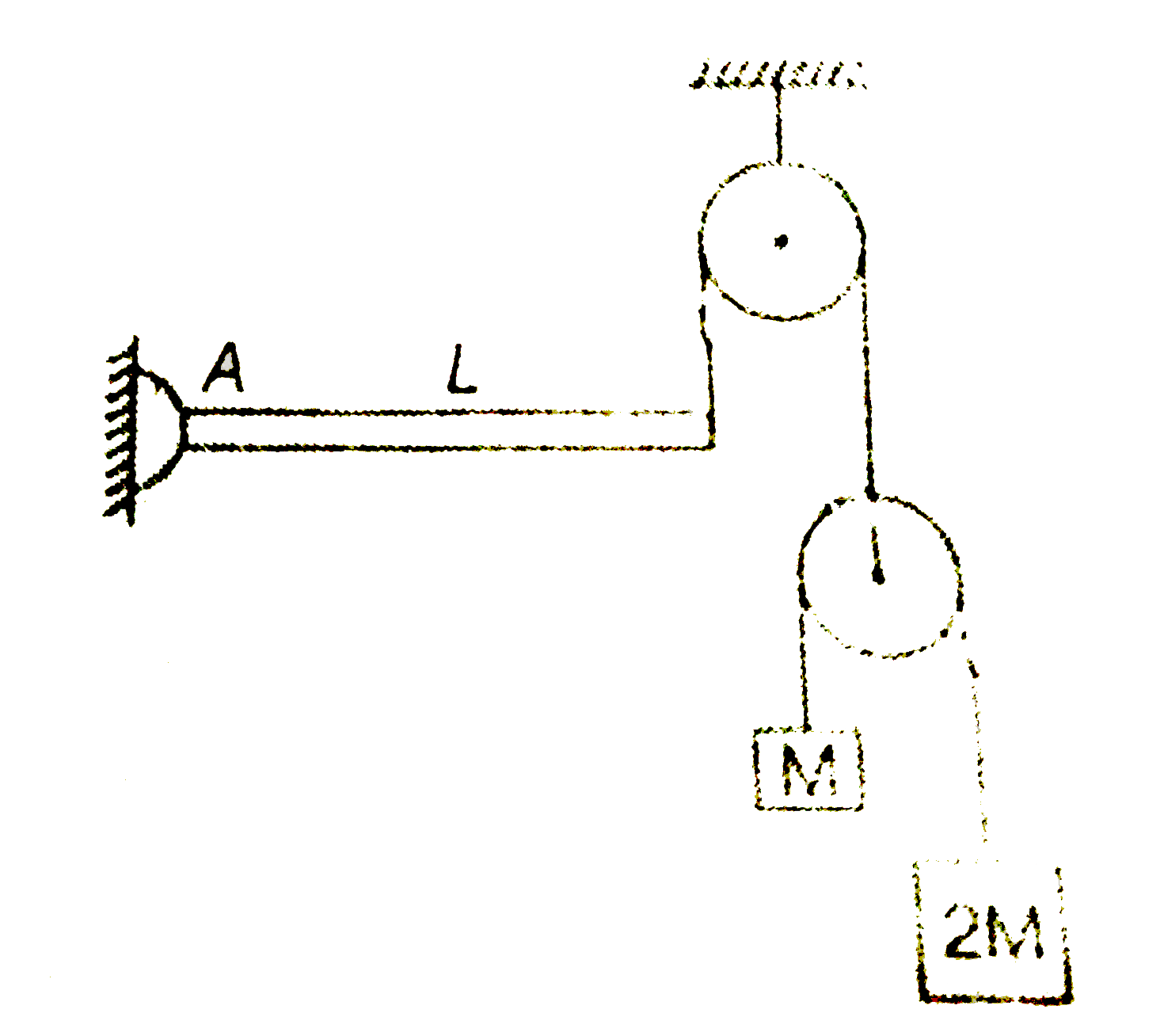
View SolutionConsider the situation shown in the figure. Uniform rod of length L can rotat freely about the hinge A in vertical plane. Pulleys and stringa are light and frictionless. If the rod remains horizontal at rest when the system is released then the mass of the rod is
View SolutionA particle of mass of mass m is attached to a light rod of lenght l other end of the rod is hinged to a wall . Minimumm velocity (Vo) that should be given to a particle in lowest positiion so that it completes a vertical circle
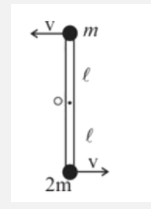
View SolutionTwo particles of masses m and 2m are attached to the massless rod of length 2l as shown in figure. The rod is hinged at its midpoint O and is free to rotate in vertical plane about hinge. The minimum speed v at the given instant so that it can complete the circle.
View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical

View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionTwo point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
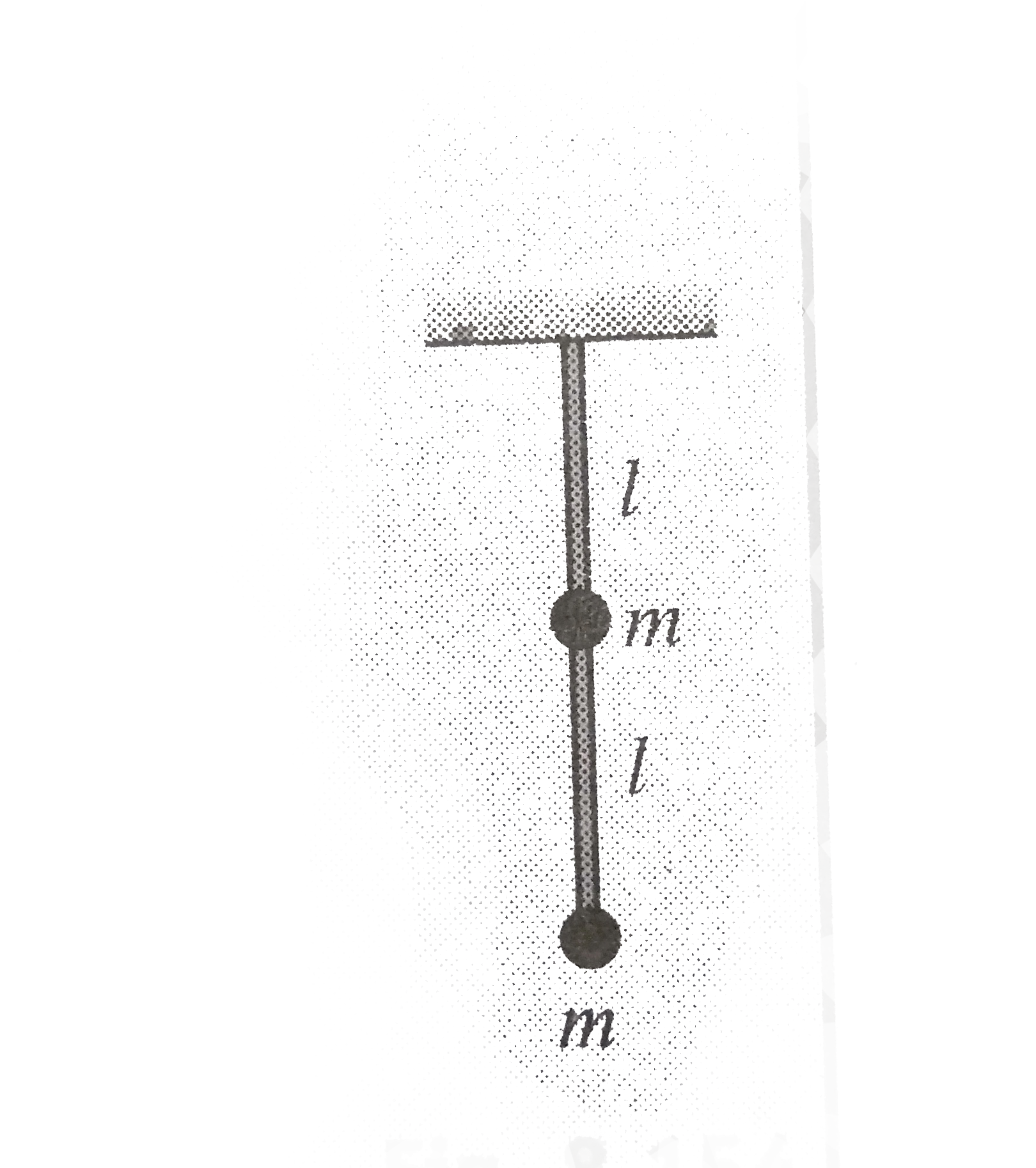
View Solution
