If a force is applied to an object, away from its centre of mass, it tends to rotate the object.
Step by step video & image solution for If a force is applied to an object, away from its centre of mass, it tends to rotate the object. by Physics experts to help you in doubts & scoring excellent marks in Class 8 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - FORCE AND PRESSURE EXERCISE - Exercises (Section I) Choose the correct option to fill in the blank.6videos
FORCE AND PRESSURE
- BOOK - ICSECHAPTER - FORCE AND PRESSURE EXERCISE - Exercises (Section II) Give reasons for the following6videos
FORCE AND PRESSURE
- BOOK - ICSECHAPTER - FORCE AND PRESSURE EXERCISE - Exercises (Section I) Choose the correct option6videos
FORCE AND PRESSURE
- BOOK - ICSECHAPTER - ENERGYEXERCISE - THEME ASSIGNMENT4videos
ENERGY
- BOOK - ICSECHAPTER - HEAT TRANSFER EXERCISE - Picture Study2videos
HEAT TRANSFER
Similar Questions
The inertia of an object tends to cause the object
View SolutionWhen force applied on an object causes it to moves in the direction of force
View SolutionWhen a force is applied on an object and if the body moves in the direction of applied force, work is said to be done.
View SolutionTwo objects are at rest on a level frictionless surface. The objects are not connected. A force F is applied to one of the objects, which then moves with acceleration a. Mark the correct statement(s).
View SolutionTwo object are initially at rest on a frictionless surface. Object 1 has a greater mass than object 2. The same constant force start to act on each object. The force is removed from each object after it accelerates over a distance d. after the force is removed from both objects, which statement is correct (p:momentum, K: kinetic energy)?
View SolutionA force F=(xˆi+2yˆj)N is applied on an object of mass 10 kg, Force displaces the object from position A(1, 0) m to position B(3, 3) m then the work done by the force is (x and y are meter)
View Solution_E01_059_Q01.png)
An object of weight W has a uniform rectangular cross section of a x2a and density of 0.25g/cm3 part of it is immersed in water and the rectangle is tilted by 45∘− while one of its corners is just at the water surface find the torque of the buoyancy force to the centre of mass of the object.View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
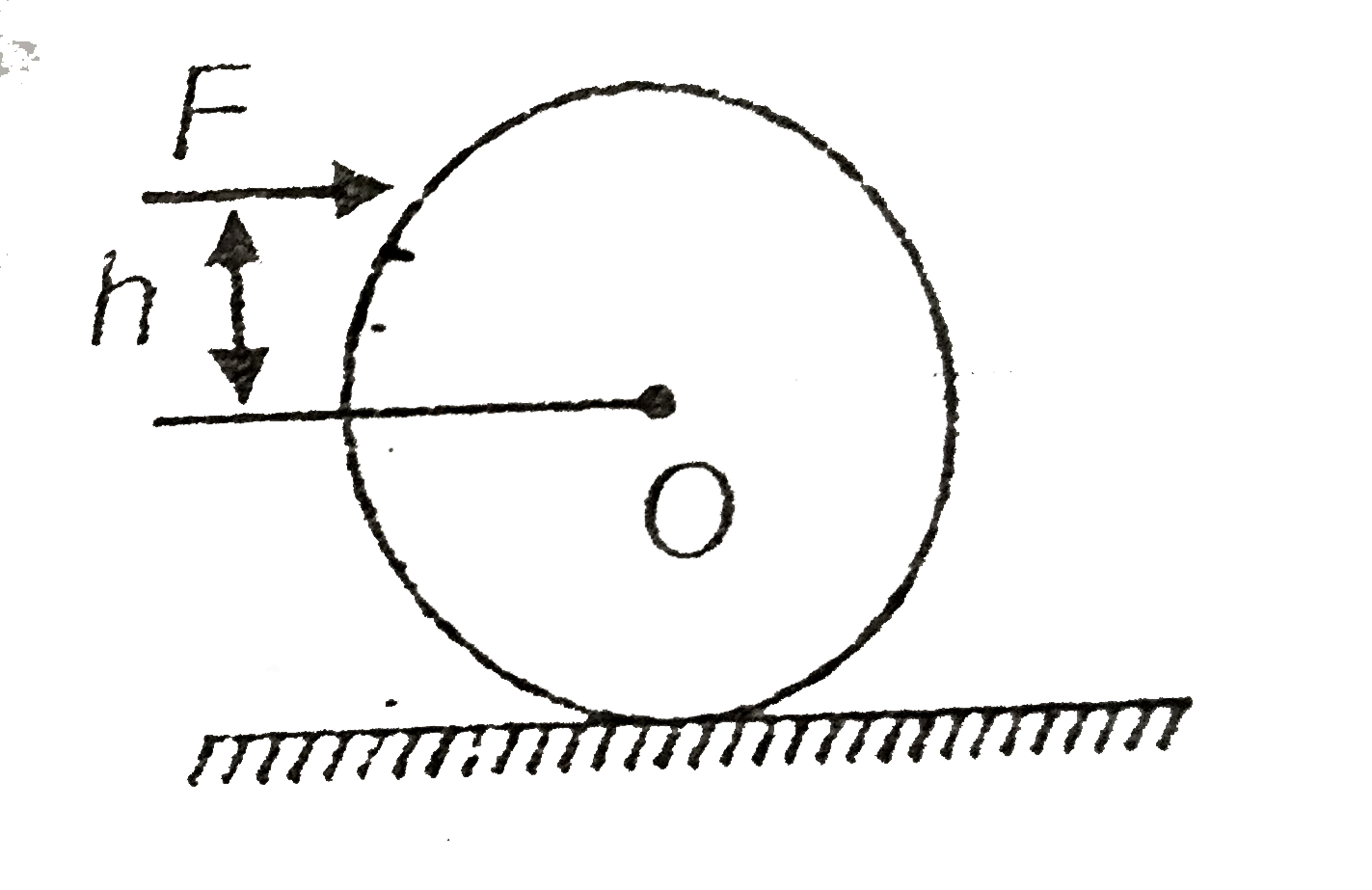
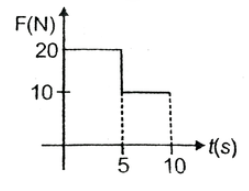
View SolutionForce is applied on an object of mass 2 kg at rest on a frictionless horizontal surface as shown in the graph. The speed of object at t=10 s will be
View SolutionIf an object is placed at the centre of a glass sphere and it is seen from outside, then prove that its virtual image is also formed at centre.
View Solution