The pendulum has .. .............. (minimum/maximum) speed at the mean position.
To determine whether the pendulum has minimum or maximum speed at the mean position, we can analyze the motion of the pendulum in terms of energy conservation.
1. Understanding the Pendulum Motion:
- A pendulum swings back and forth around a central point known as the mean position. The motion consists of two extreme points (maximum height) and the mean position (lowest point).
Hint: Visualize the pendulum's swing and identify the mean position and extreme points.
2. Energy Conservation in Pendulum:
- The total mechanical energy of the pendulum is conserved. This means that the sum of potential energy (PE) and kinetic energy (KE) remains constant throughout the motion.
Hint: Remember that energy conservation implies that energy can transform from one form to another but the total remains the same.
3. Energy at Extreme Points:
- At the extreme points of the swing, the pendulum is momentarily at rest. Therefore, its speed (velocity) is zero. At this point, all the energy is potential energy (PE), and kinetic energy (KE) is zero.
Hint: Think about what happens to the pendulum when it reaches the highest point of its swing.
4. Energy at Mean Position:
- At the mean position, the pendulum is at its lowest point. Here, the potential energy is at its minimum (zero), and the kinetic energy is at its maximum because the pendulum is moving the fastest.
Hint: Consider how the height of the pendulum affects its potential energy.
5. Conclusion:
- Since the kinetic energy is maximum at the mean position, it follows that the speed of the pendulum is also maximum at this point.
Final Answer: The pendulum has maximum speed at the mean position.
- A pendulum swings back and forth around a central point known as the mean position. The motion consists of two extreme points (maximum height) and the mean position (lowest point).
- The total mechanical energy of the pendulum is conserved. This means that the sum of potential energy (PE) and kinetic energy (KE) remains constant throughout the motion.
- At the extreme points of the swing, the pendulum is momentarily at rest. Therefore, its speed (velocity) is zero. At this point, all the energy is potential energy (PE), and kinetic energy (KE) is zero.
- At the mean position, the pendulum is at its lowest point. Here, the potential energy is at its minimum (zero), and the kinetic energy is at its maximum because the pendulum is moving the fastest.
- Since the kinetic energy is maximum at the mean position, it follows that the speed of the pendulum is also maximum at this point.
Topper's Solved these Questions
- WORK AND ENERGYBOOK - ICSECHAPTER - WORK AND ENERGYEXERCISE - Exercises (Name the following)
8 Videos
- WORK AND ENERGYBOOK - ICSECHAPTER - WORK AND ENERGYEXERCISE - Exercises (Choose the correct option)
6 Videos
- WORK AND ENERGYBOOK - ICSECHAPTER - WORK AND ENERGYEXERCISE - Questions (Write T for True and F for False. Correct the false statements)
5 Videos
- SOUNDBOOK - ICSECHAPTER - SOUNDEXERCISE - Picture Study
4 Videos
Similar Questions
Minimum solute potential means
View SolutionThe figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
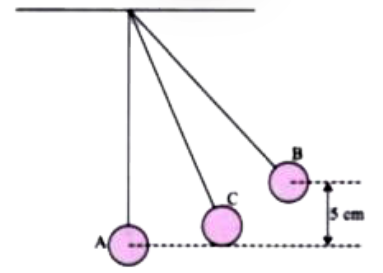
(i) What is the potential energy of the pendulum at the position B?
(ii) What is the total mechanical energy at point C?
(iii) What is the speed of the bob at the position A when released from B ?
(Take g = 10ms−2 and there is no loss of energy.)
View Solution
Knowledge Check
In an oscillating pendulum the ............... energy is maximum at extremes.
ApotentialBvibrationalCgravitational potentialDkineticConsider the following statements in relation to the motion of a simple pendulum :
(1) The acceleration is always directed towards the mean position
(2) the maximum acceleration occurs at the mean position
(3) The maximum velocity occurs at the mean position
(4) The magnitude of maximum acceleration is equal to the maximum velocity
Which of the following statements are correct ?A1 and 2B1 and 3C3 and 4D2 and 4
Statement-1 : As a simple pendulum oscillates, its bob has a non-zero acceleration at the mean position which is directed towards the point of suspension.
bacause
Statement -2 : Speed of an object in SHM is maximum at the mean position.
View SolutionName the type of energy possessed by the bob of a simple pendulum when it is at (a) the extreme position, (b) the mean position, and (c) between the mean and extreme positions
View SolutionA simple pendulum suspended from the roof off a lift oscillates with frequency υ when the lift is at rest. If the lift falls freely under gravity, its frequency of oscillation becomes
View SolutionThe amplitude of a simple pendulum is 10 cm. When the pendulum is at a displacement of 4 cm from the mean position, the ratio of kinetic and potential energies at that point is
View SolutionA simple pendulum is suspended from the ceiling a car accelerating uniformly on a horizontal road. If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
View SolutionThe bob of a simple pendulum is imparted a velocity of 5 ms−1 when it is at its mean position.To what maximum vertical height will it rise on reaching at its extreme position if 60% of its energy is lost on overcoming the friction of air?
(Take g=10 m s−2)
View Solution
