In the given figure, AD is median of ΔABC and E is any point on median AD. Prove that Area (ΔABE) = Area (ΔACE)
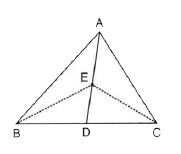
Step by step video & image solution for In the given figure, AD is median of DeltaABC and E is any point on median AD. Prove that Area (DeltaABE) = Area (DeltaACE) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )22videos
AREA THEOREMS
- BOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(A)36videos
AREA THEOREMS
- BOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)12videos
AREA AND PERIMETER OF PLANE FIGURES
- BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA12videos
CHAPTER REVISION (STAGE 2)
Similar Questions
In the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)
 View Solution
View SolutionIn the given figure, D is mid-point of side AB of △ABC and BDEC is a parallelogram.
Prove that :
Area of ΔABC = Area of //gmBDEC
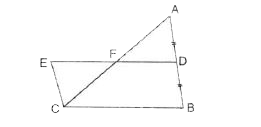 View Solution
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2ADView SolutionIn the figure of question 2, if E is the mid point of median AD, then prove that :
Area(ΔABE)=14Area(ΔABC).
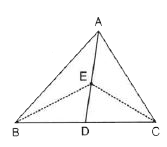 View Solution
View SolutionIn the figure of question 2, if E is the mid point of median AD, then prove that :
Area(ΔABE)=14Area(ΔABC).
 View Solution
View SolutionIn the given figures, AB > AC and D is any point on BC.
Prove that : AB >AD.
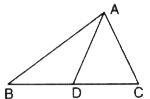 View Solution
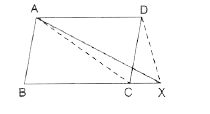
View SolutionIn the given figure, ABCD is a parallelogram BC is produced to point X. prove that :
area(ΔABX)=area( .ACXD)
 View Solution
View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABCView SolutionIn the adjoining figure, DE∣∣BC. Prove that area (ΔACD)= area (ΔABE)
 View Solution
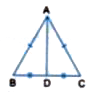
View SolutionIn the adjoining figure, ΔABC is an isosceles triangles in which AB=AC and AD is a median. Prove that :
(i) ΔADB≅ΔADC
(ii) ∠BAD=∠CAD
 View Solution
View Solution

