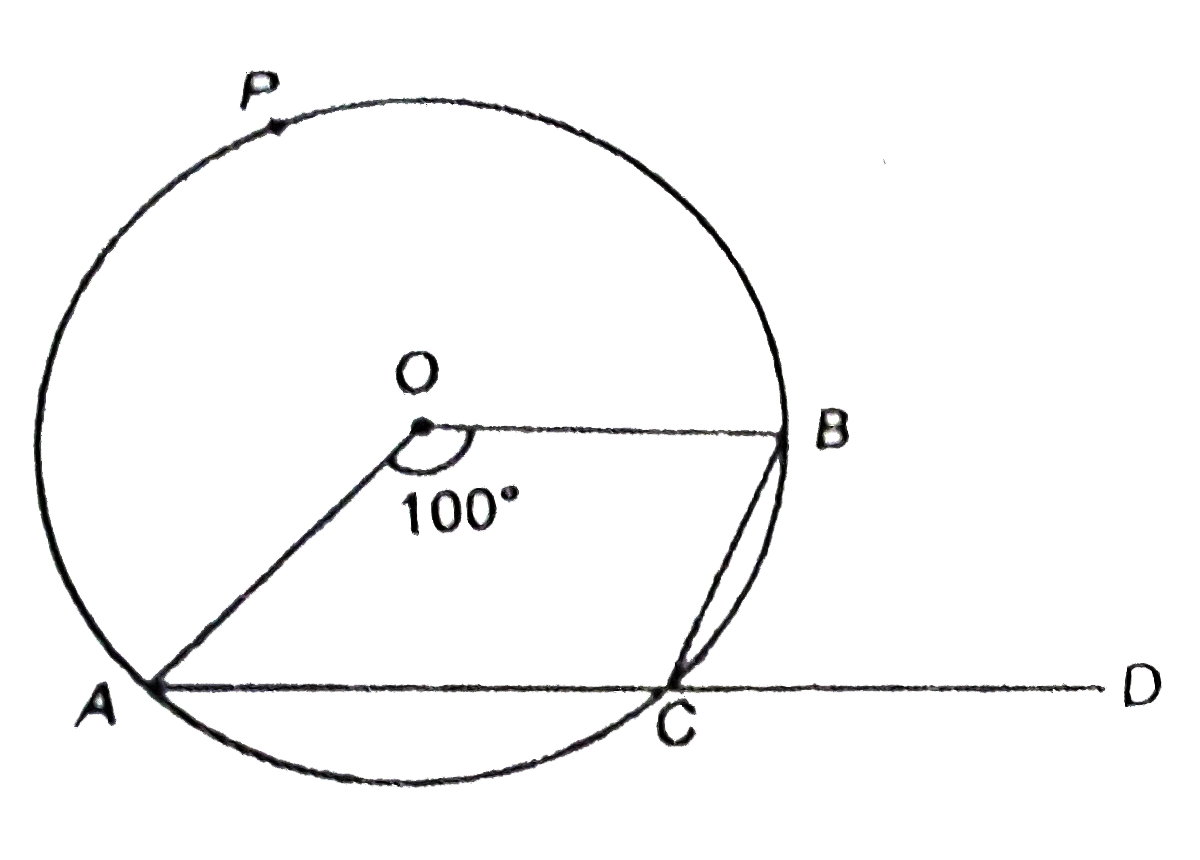
In the given figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC.
if ∠AOB=100∘ find ∠BOC
To solve the problem, we need to find the angle ∠BOC given that the length of arc AB is twice the length of arc BC and that ∠AOB=100∘.
1. Understanding the relationship between arcs and angles:
- The length of an arc in a circle is directly proportional to the angle subtended by that arc at the center of the circle. Therefore, if the length of arc AB is twice that of arc BC, the angle subtended by arc AB will also be twice that of arc BC.
2. Let the angle subtended by arc BC be x:
- Since the angle AOB=100∘, we can express the relationship as:
∠AOB=∠AB+∠BOC
- We know that ∠AB=2x (because the length of arc AB is twice that of arc BC).
3. Setting up the equation:
- The total angle at the center O is:
∠AOB+∠BOC=100∘+x
- Since ∠AOB=2x, we can write:
2x+x=100∘
- This simplifies to:
3x=100∘
4. Solving for x:
- Dividing both sides by 3 gives:
x=100∘3≈33.33∘
5. Finding ∠BOC:
- Since ∠BOC=x, we have:
∠BOC=100∘3≈33.33∘
Final Answer:
∠BOC≈33.33∘
- The length of an arc in a circle is directly proportional to the angle subtended by that arc at the center of the circle. Therefore, if the length of arc AB is twice that of arc BC, the angle subtended by arc AB will also be twice that of arc BC.
- Since the angle AOB=100∘, we can express the relationship as:
∠AOB=∠AB+∠BOC
- We know that ∠AB=2x (because the length of arc AB is twice that of arc BC).
- The total angle at the center O is:
∠AOB+∠BOC=100∘+x
- Since ∠AOB=2x, we can write:
2x+x=100∘
- This simplifies to:
3x=100∘
- Dividing both sides by 3 gives:
x=100∘3≈33.33∘
- Since ∠BOC=x, we have:
∠BOC=100∘3≈33.33∘
∠BOC≈33.33∘
Topper's Solved these Questions
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(B)
15 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA
11 Videos
- CIRCLES BOOK - ICSECHAPTER - CIRCLES EXERCISE - TOPIC-2
25 Videos
Similar Questions
Knowledge Check
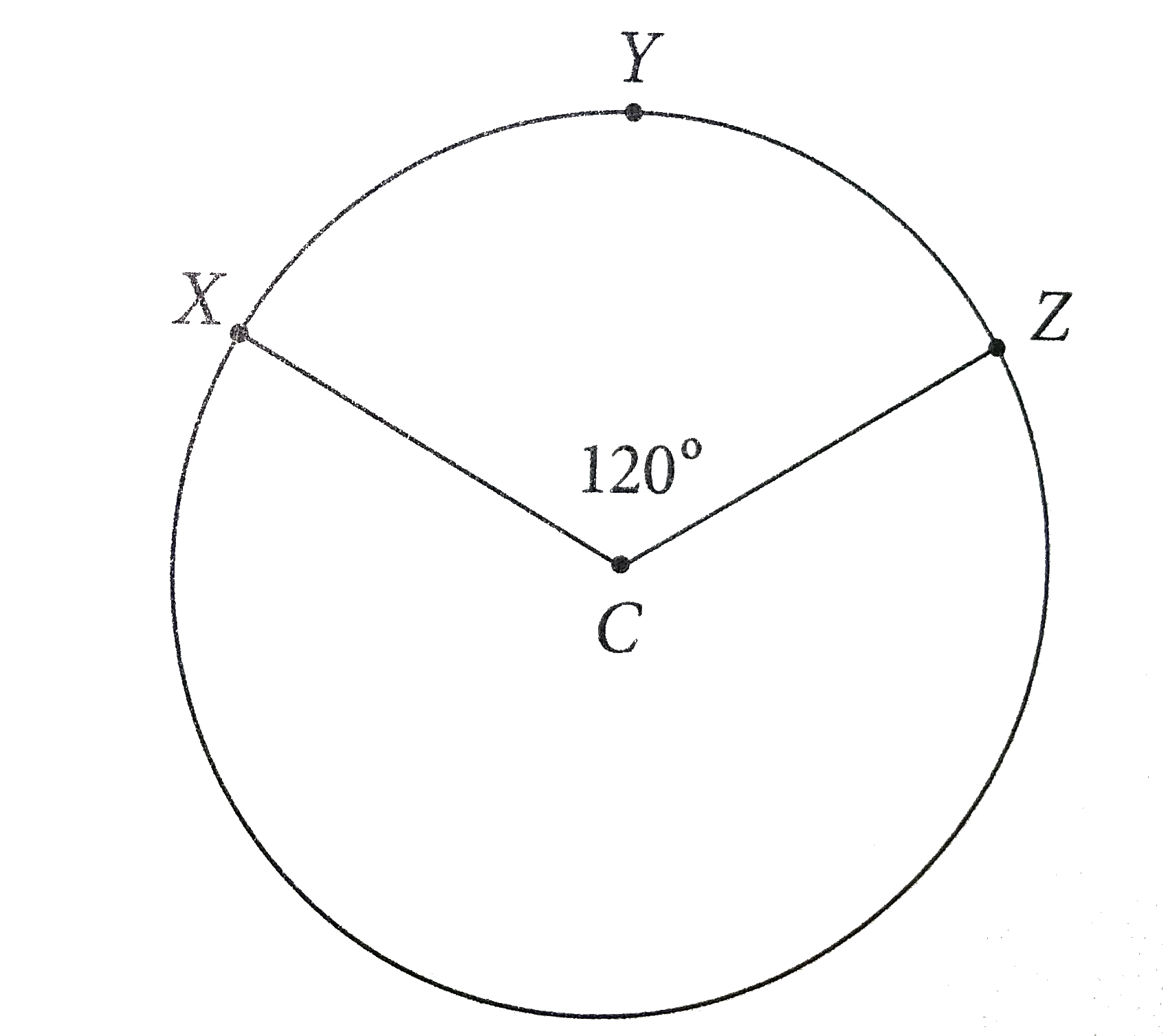
In the figure above, C is the center of a circle. If the length of the arc XYZ is 4π, what is the radius of the circle?A4B2√3C6D12
In Figure, O is the centre of the circle and the measure of arc ABC is 1000. Determine ∠ADC and ∠ABC
View SolutionIn the given the length of arcs AB and BC are in the ratio 3:2.
If ∠AOB=96∘ find
∠BOC
View SolutionIn the adjoining figure , O is the centre of the circle. If ∠ACB=25∘, then find ∠AOB.
View SolutionIn figure ΔABC is circumscribing a circle. Find the length of BC
View SolutionIn the given the length of arcs AB and BC are in the ratio 3:2.
If ∠AOB=96∘ find
∠ABC
View SolutionIn the given figure, O is the centre of a circle, AB is a side of regular octagon and AC is a side of regular hexagon. Find :

∠AOB
View SolutionIn the given figure , the lengths of arc AB and are BC arc in the ratio 3: 2 if ∠AOB=96∘, find
(i)∠CAB(ii)∠ADB

View Solution