In the given the length of arcs AB and BC are in the ratio 3:2.
If ∠AOB=96∘ find
∠ABC
The correct Answer is:100∘)
To solve the problem step-by-step, we will follow the reasoning laid out in the video transcript.
Step 1: Understand the Given Information
We are given that the lengths of arcs AB and BC are in the ratio of 3:2, and the angle AOB is 96 degrees. We need to find the angle ABC.
Step 2: Relate the Angles to the Arcs
Since the lengths of the arcs are in the ratio of 3:2, the angles subtended by these arcs at the center of the circle (angle AOB and angle BOC) will also be in the same ratio.
Let:
- Angle AOB = 3x
- Angle BOC = 2x
From the problem, we know that:
3x=96∘
Step 3: Solve for x
To find x, we can set up the equation:
x=96∘3=32∘
Step 4: Find Angle BOC
Now we can find angle BOC:
BOC=2x=2×32∘=64∘
Step 5: Analyze Triangle OBC
In triangle OBC, since OB = OC (both are radii of the circle), angles OBC and OCB are equal. Let:
- Angle OBC = Angle OCB = y
Using the angle sum property of triangles:
OBC+OCB+BOC=180∘
y+y+64∘=180∘
2y+64∘=180∘
2y=180∘−64∘
2y=116∘
y=58∘
Step 6: Analyze Triangle OAB
In triangle OAB, we know:
- Angle AOB = 96 degrees
- Angles OAB and OBA are equal (let's call them z).
Using the angle sum property again:
OAB+OBA+AOB=180∘
z+z+96∘=180∘
2z+96∘=180∘
2z=180∘−96∘
2z=84∘
z=42∘
Step 7: Find Angle ABC
Finally, angle ABC can be found by adding angles OAB and OBC:
ABC=OAB+OBC=42∘+58∘=100∘
Conclusion
Thus, the angle ABC is:
Angle ABC=100∘
---
We are given that the lengths of arcs AB and BC are in the ratio of 3:2, and the angle AOB is 96 degrees. We need to find the angle ABC.
Since the lengths of the arcs are in the ratio of 3:2, the angles subtended by these arcs at the center of the circle (angle AOB and angle BOC) will also be in the same ratio.
- Angle AOB = 3x
- Angle BOC = 2x
3x=96∘
To find x, we can set up the equation:
x=96∘3=32∘
Now we can find angle BOC:
BOC=2x=2×32∘=64∘
In triangle OBC, since OB = OC (both are radii of the circle), angles OBC and OCB are equal. Let:
- Angle OBC = Angle OCB = y
OBC+OCB+BOC=180∘
y+y+64∘=180∘
2y+64∘=180∘
2y=180∘−64∘
2y=116∘
y=58∘
In triangle OAB, we know:
- Angle AOB = 96 degrees
- Angles OAB and OBA are equal (let's call them z).
OAB+OBA+AOB=180∘
z+z+96∘=180∘
2z+96∘=180∘
2z=180∘−96∘
2z=84∘
z=42∘
Finally, angle ABC can be found by adding angles OAB and OBC:
ABC=OAB+OBC=42∘+58∘=100∘
Thus, the angle ABC is:
Angle ABC=100∘
Topper's Solved these Questions
Similar Questions
In the given the length of arcs AB and BC are in the ratio 3:2.
If ∠AOB=96∘ find
∠BOC
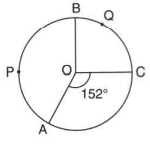
View SolutionIn the given figure, lengths of arcs APB and BQC are in the ratio 5:3 and angle AOC=152∘, find angle ACB and angle BAC.
View SolutionIn the given figure , the lengths of arc AB and are BC arc in the ratio 3: 2 if ∠AOB=96∘, find
(i)∠CAB(ii)∠ADB

View SolutionIn circle given below . O is its centre and lengths of chords AB and CD are in the ratio 5 :3
If angle AOB = 100∘, find :
(i)∠COD

View SolutionIn the given figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC.
if ∠AOB=100∘ find ∠BOC
View SolutionIn the given 'O' is the centre of the circle, Arc AB=ArcBC=Cd.If∠OAB=48∘, find:
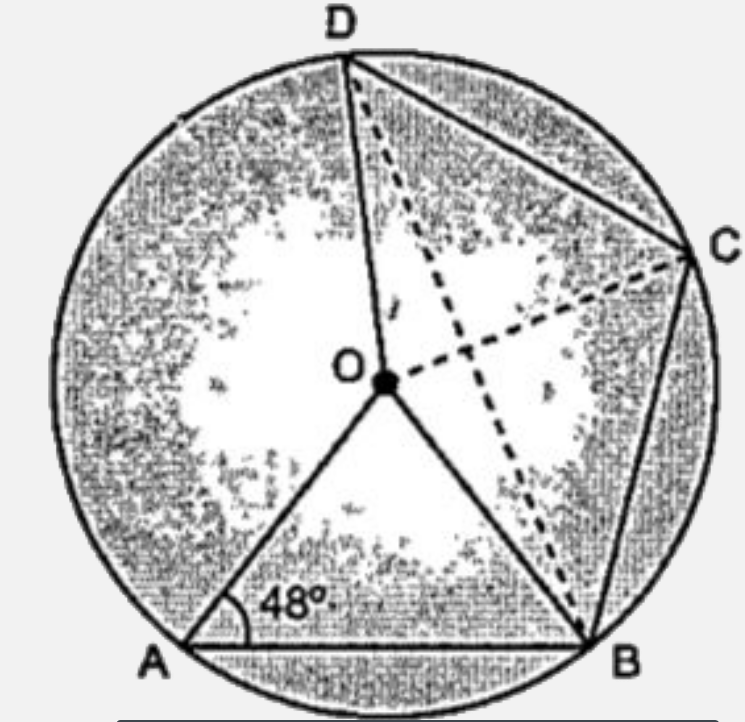
∠OBD
View SolutionIn the given circle. Arc APB and are BQC are in the ratio 2: 5 and O is centre of the circle.
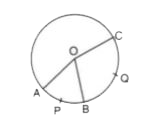
If angle AOB = 44∘ : Find angle AOC.
View SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠OAC
View SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠BOC
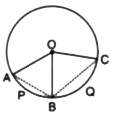
View SolutionIn the given figure , arc APB : arc BQC = 2: 3 and ∠AOC=150∘, Find :
(i) ∠AOB
(ii) ∠BOC
(iii) ∠OBA
(iv) ∠OCB
(v) ∠ABC
View Solution
