In a cricle of radius 10 cm, AB and CD are two parallel chords of lengths 16 cm and 12 cm respectively. Calculate the distance between the chords, if they are on :
the same side of the centre.
To solve the problem of finding the distance between the two parallel chords AB and CD in a circle of radius 10 cm, we will follow these steps:
Step 1: Identify the Circle and Chords
We have a circle with a radius of 10 cm. The lengths of the chords are given as:
- Length of chord AB = 16 cm
- Length of chord CD = 12 cm
Step 2: Find the Midpoints of the Chords
Let O be the center of the circle. The midpoints of the chords are:
- Let M be the midpoint of chord AB.
- Let N be the midpoint of chord CD.
Step 3: Calculate the Distances from the Center to the Midpoints
Using the property of chords in a circle, we can find the distances from the center O to the midpoints M and N.
For Chord AB:
1. The length of chord AB is 16 cm, so the distance from the center O to the midpoint M (OM) can be calculated using the Pythagorean theorem.
2. The half-length of chord AB = 16 cm / 2 = 8 cm.
3. Using the Pythagorean theorem:
OA2=OM2+AM2
where OA is the radius (10 cm) and AM is half the length of the chord (8 cm).
102=OM2+82
100=OM2+64
OM2=100−64=36
OM=√36=6 cm
For Chord CD:
1. The length of chord CD is 12 cm, so the distance from the center O to the midpoint N (ON) can also be calculated using the Pythagorean theorem.
2. The half-length of chord CD = 12 cm / 2 = 6 cm.
3. Using the Pythagorean theorem:
OC2=ON2+CN2
where OC is the radius (10 cm) and CN is half the length of the chord (6 cm).
102=ON2+62
100=ON2+36
ON2=100−36=64
ON=√64=8 cm
Step 4: Calculate the Distance Between the Chords
Since both chords are on the same side of the center, the distance (D) between the chords can be calculated as:
D=OM−ON
Substituting the values we found:
D=8 cm−6 cm=2 cm
Final Answer
The distance between the two parallel chords AB and CD is 2 cm.
---
We have a circle with a radius of 10 cm. The lengths of the chords are given as:
- Length of chord AB = 16 cm
- Length of chord CD = 12 cm
Let O be the center of the circle. The midpoints of the chords are:
- Let M be the midpoint of chord AB.
- Let N be the midpoint of chord CD.
Using the property of chords in a circle, we can find the distances from the center O to the midpoints M and N.
1. The length of chord AB is 16 cm, so the distance from the center O to the midpoint M (OM) can be calculated using the Pythagorean theorem.
2. The half-length of chord AB = 16 cm / 2 = 8 cm.
3. Using the Pythagorean theorem:
OA2=OM2+AM2
where OA is the radius (10 cm) and AM is half the length of the chord (8 cm).
102=OM2+82
100=OM2+64
OM2=100−64=36
OM=√36=6 cm
1. The length of chord CD is 12 cm, so the distance from the center O to the midpoint N (ON) can also be calculated using the Pythagorean theorem.
2. The half-length of chord CD = 12 cm / 2 = 6 cm.
3. Using the Pythagorean theorem:
OC2=ON2+CN2
where OC is the radius (10 cm) and CN is half the length of the chord (6 cm).
102=ON2+62
100=ON2+36
ON2=100−36=64
ON=√64=8 cm
Since both chords are on the same side of the center, the distance (D) between the chords can be calculated as:
D=OM−ON
Substituting the values we found:
D=8 cm−6 cm=2 cm
The distance between the two parallel chords AB and CD is 2 cm.
Topper's Solved these Questions
Similar Questions
In a cricle of radius 10 cm, AB and CD are two parallel chords of lengths 16 cm and 12 cm respectively. Calculate the distance between the chords, if they are on :
the opposite sides of the centre.
View SolutionIn a circle of radius 5 cm, PQ and RS are two parallel chords of lengths 8 cm and 6 cm respectively. Calculate the distance between the chords if they are on:
the same side of the centre.
View SolutionIn a circle of radius 5 cm, PQ and RS are two parallel chords of lengths 8 cm and 6 cm respectively. Calculate the distance between the chords if they are on:
opposite sides of the centre.
View SolutionIn a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords, if both the chords are :
on the same side of the centre
View SolutionIn a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords, if both the chords are :
on the opposite sides of the centre,
View SolutionIn a circle of radius 17 cm, two parallel chord of length 30 cm and 16 cm are drawn, find the distance between the chords, if both the chords are :
On the opposite sides of the centre,
View SolutionThe diameter of a circle is 20 cm. There are two parallel chords of length 16 cm . And 12 cm. Find the distance between these chords if chords are on the:
(i) same side
(ii) opposite side of the centre.
View SolutionFind the area of a trapezium whose parallel sides are of lengths 10cm and 12cm and the distance between them is 4cm.
View SolutionTwo parallel chords of a circle , 12 cm and 16 cm long are on the same of the centre. The distance between them is 2 cm. Find the radius of the circle.
View SolutionIn the adjoining figure ,AB and CD are two parallel chords of a circle with centre O , whose length are 16 cm and 12 cm respectively. Find the radius of the circle if the distance between them is 14 cm.
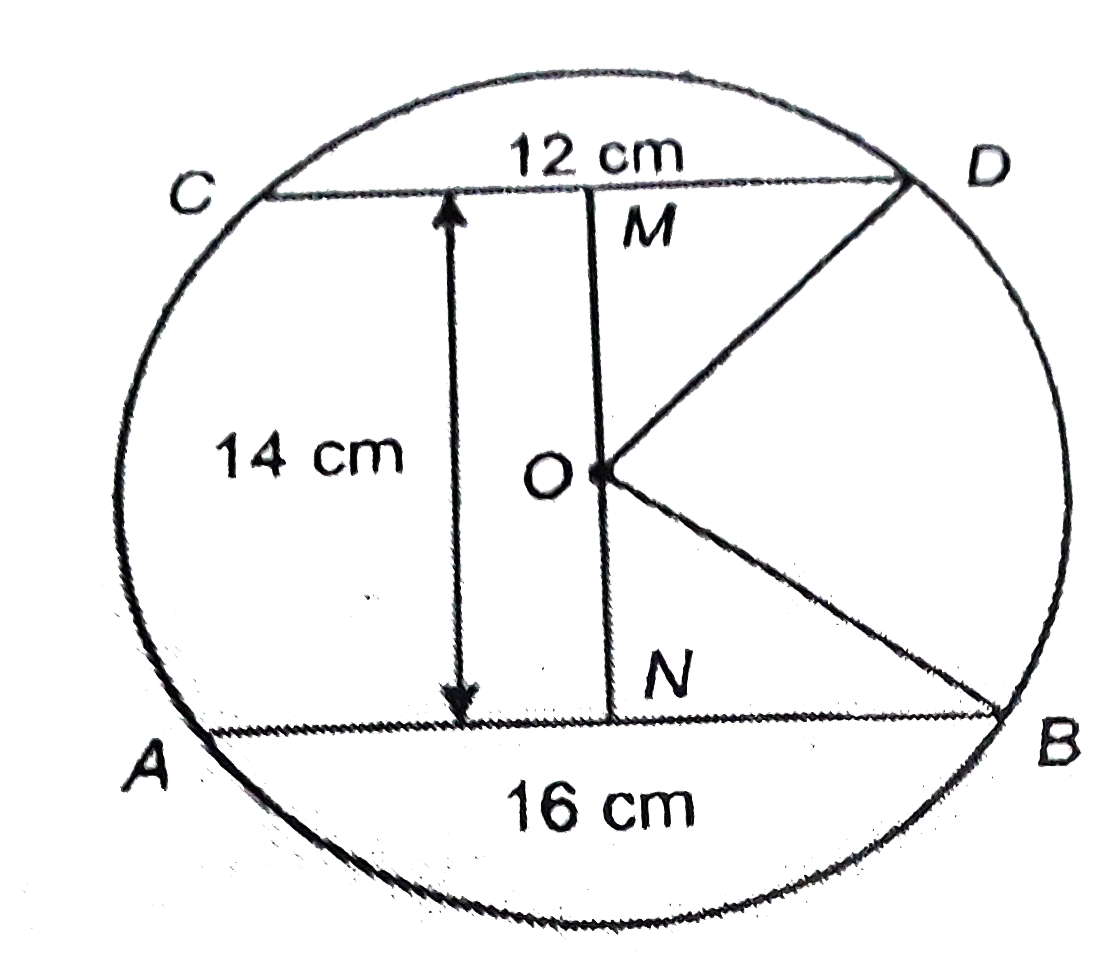
View Solution