Given two equal chords AB and CD of a circle, with centre O, intersecting each other at point p prove that

BP=DP
Step by step video & image solution for Given two equal chords AB and CD of a circle, with centre O, intersecting each other at point p prove that BP=DP by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
View SolutionIf chords AB and CD of a circle intersect each other at a point inside the circle, prove that : PA×PB=PC×PD .
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.

View SolutionAB and CD are two equal chords of a circle with centre O which intersect each other at right angle at point P. If OM ⊥ AB and ON ⊥ CD, show that OMPN is a square.
View SolutionAB and CD are two equal chords of a circle with centre O which intersect each other at right angle at P. If OM ⊥ AB and ON ⊥ CD, show that OMPN is a square.
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
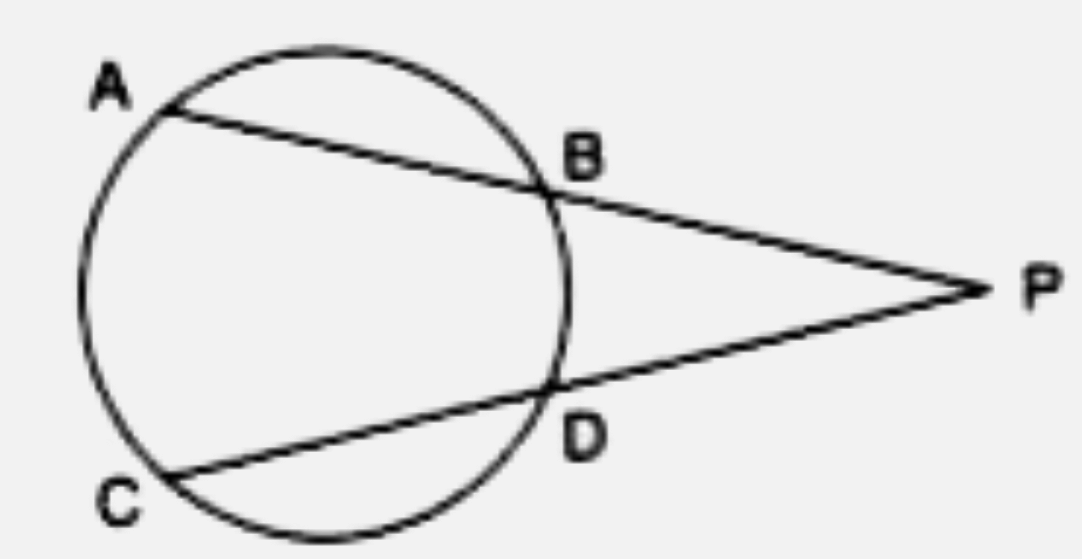
PB=PD
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :

PA=PC.
View SolutionChords AB and CD of a circle with centre O, intersect at a point E. If OE bisects angle AED, prove that chord AB = chord CD.
View SolutionIn Figure two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC~ΔPDB
(ii) PA⋅PB = PC⋅PD

View Solution