The circumference of a circle, with centre O, is divided into three arcs APB, BQC and CRA such that : arcAPB2=arcBQC3=arcCRA4 Find ∠BOC.
To solve the problem, we need to find the angle ∠BOC given that the arcs of the circle are divided in a specific ratio. Let's break down the solution step by step.
Step 1: Define the arcs in terms of angles
Let:
- arc APB=2x
- arc BQC=3x
- arc CRA=4x
Step 2: Relate the arcs to the angles at the center
Using the relationship between the length of the arc and the angle at the center, we have:
- ∠AOB=2xr
- ∠BOC=3xr
- ∠COA=4xr
Step 3: Sum of angles at the center
The sum of the angles at the center of the circle must equal 360∘:
∠AOB+∠BOC+∠COA=360∘
Substituting the expressions from Step 2:
2xr+3xr+4xr=360∘
Step 4: Simplify the equation
Combining the terms gives:
(2x+3x+4x)r=360∘
9xr=360∘
Step 5: Solve for x
Multiplying both sides by r:
9x=360∘r
Dividing by 9:
x=40∘r
Step 6: Find ∠BOC
Now, we can find ∠BOC:
∠BOC=3xr
Substituting x=40∘r:
∠BOC=3(40∘r)r=120∘
Final Answer
Thus, the angle ∠BOC is:
120∘
Let:
- arc APB=2x
- arc BQC=3x
- arc CRA=4x
Using the relationship between the length of the arc and the angle at the center, we have:
- ∠AOB=2xr
- ∠BOC=3xr
- ∠COA=4xr
The sum of the angles at the center of the circle must equal 360∘:
∠AOB+∠BOC+∠COA=360∘
Substituting the expressions from Step 2:
2xr+3xr+4xr=360∘
Combining the terms gives:
(2x+3x+4x)r=360∘
9xr=360∘
Multiplying both sides by r:
9x=360∘r
Dividing by 9:
x=40∘r
Now, we can find ∠BOC:
∠BOC=3xr
Substituting x=40∘r:
∠BOC=3(40∘r)r=120∘
Thus, the angle ∠BOC is:
120∘
Topper's Solved these Questions
Similar Questions
Knowledge Check

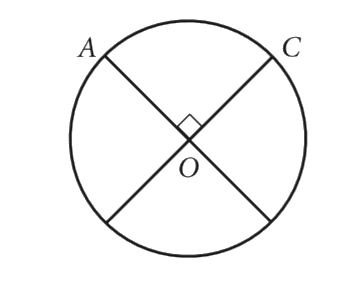
In the circle with center O, OD=BD and arc DB=2π. What is the area of the circle?A36πB16πC12πD4π
The circle above with center O has a circumference of 36. What is the length of minor arc AB⌢
View Solution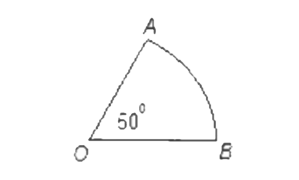
In the figure abvoe, aB is the arc of a circle with centre O. If the length of arc AB is 4π, what is the area of region OAB to the nearest tenth?
View SolutionBC is a chord with centre O. A is a point on an arc BC . Prove that: ∠BAC+∠OBC= 90 , if A is the point on the major arc.
View SolutionWrite the truth value (T/F) of the following with suitable reasons: A circle is a plane figure. Line segment joining the centre to any point on the circle is a radius of the circle. If a circle is divided into three equal arcs each is a major arc. A circle has only finite number of equal chords. A chord of a circle, which is twice as long is its radius is a diameter of the circle. Sector is the region between the chord and its corresponding arc. The degree measure of an arc is the complement of the central angle containing the arc. The degree measure of a semi-circle is 1800
View SolutionThe radius of a circle is 3.6 cm. Find the length of the arc of the sector with central angle 36∘
View SolutionIn the given circle. Arc APB and are BQC are in the ratio 2: 5 and O is centre of the circle.

If angle AOB = 44∘ : Find angle AOC.
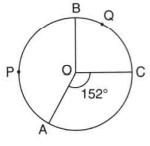
View SolutionIn the given figure, lengths of arcs APB and BQC are in the ratio 5:3 and angle AOC=152∘, find angle ACB and angle BAC.
View Solution