Points P (2, 7) is the centre of a circle with radius 13 unit, PT is perpendicular to chord AB and T = (-2, -4), Calculate the length of ,

(i) AT
(ii) AB.
The correct Answer is:(i) 12 unit (ii) 24 unit
Step by step video & image solution for Points P (2, 7) is the centre of a circle with radius 13 unit, PT is perpendicular to chord AB and T = (-2, -4), Calculate the length of , (i) AT (ii) AB. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - DISTANCE FORMULAEXERCISE - EXERCISE 551videos
DISTANCE FORMULA
- BOOK - ICSECHAPTER - DISTANCE FORMULAEXERCISE - EXERCISE 561videos
DISTANCE FORMULA
- BOOK - ICSECHAPTER - DISTANCE FORMULAEXERCISE - EXERCISE 531videos
DISTANCE FORMULA
- BOOK - ICSECHAPTER - CONSTRUCTION OF POLYGONSEXERCISE - Exercise 1576videos
CONSTRUCTION OF POLYGONS
- BOOK - ICSECHAPTER - EXPANSIONSEXERCISE - 4 Marks questions10videos
EXPANSIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
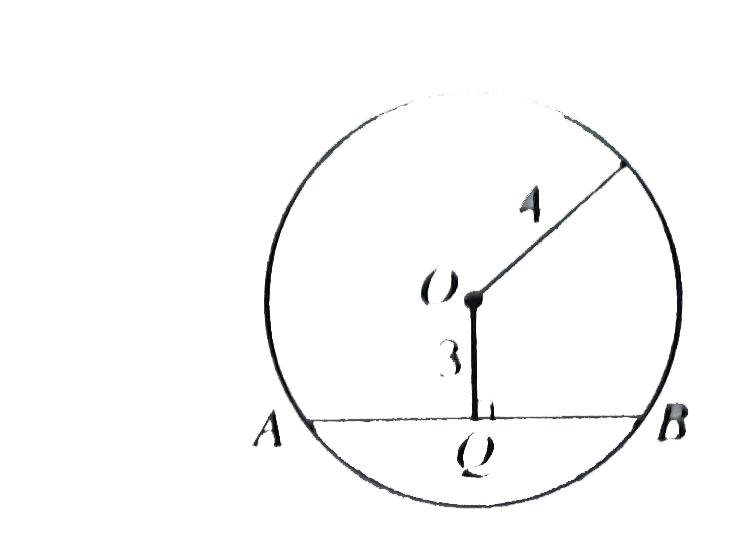
A chord ¯¯¯¯¯¯AB is 3 cm. from the center of a circle with radius 4. What is the length of chord ¯¯¯¯¯¯AB ?A√7B2√7C5D10
O is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
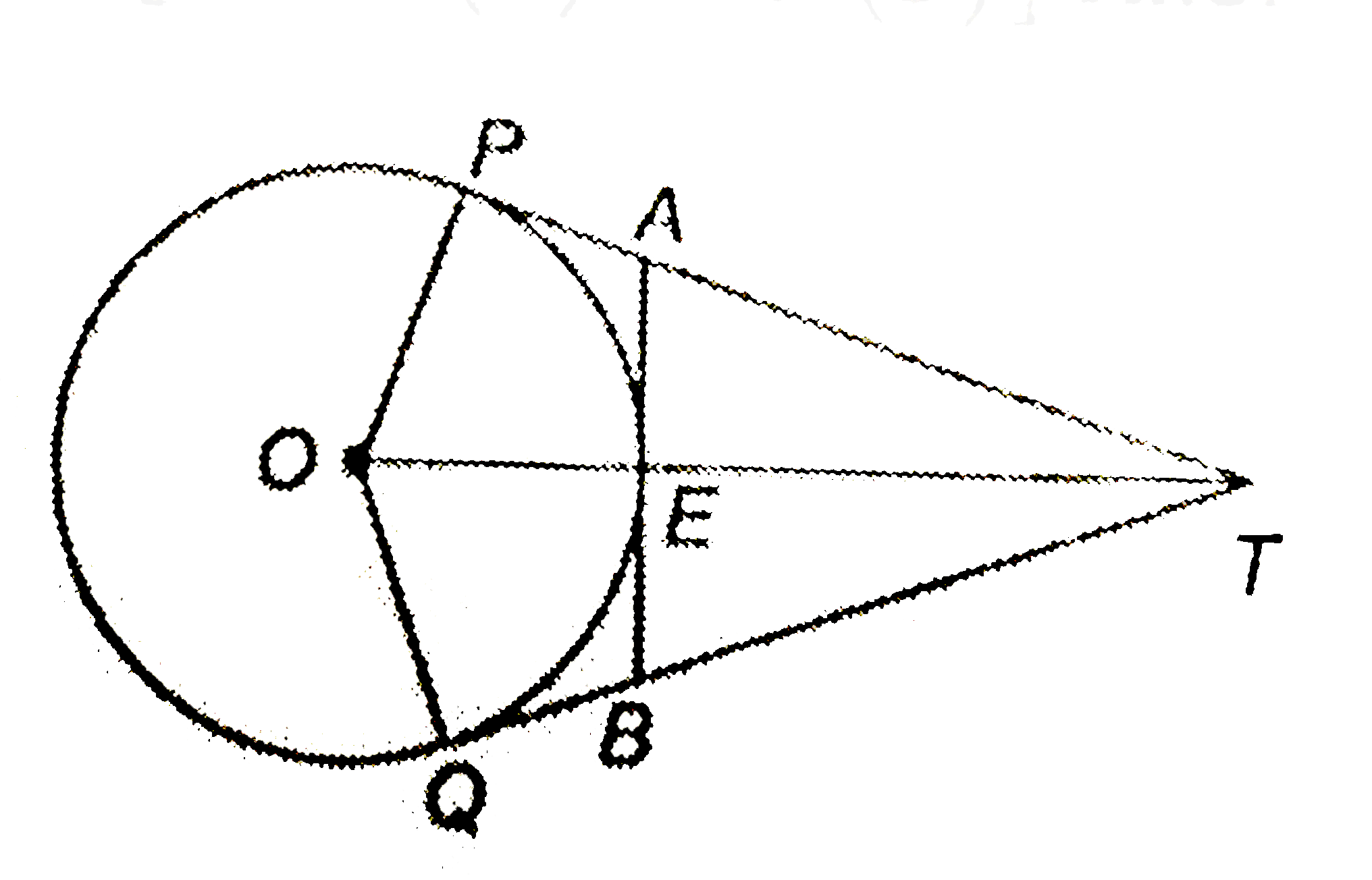 View Solution
View SolutionThe radius of a circle is 17-0 cm and the length of perpendicular drawn from its centre to a chord is 8 0 cm. Calculate the length of the chord.
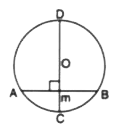
View SolutionIn the given figure, the diameter CD of a circle with centre 0 is perpendicular to the chord AB.
If AB = 8 cm and CM = 2 cm, find the radius of the circle.
 View Solution
View SolutionIn the adjoining figure, 'O' is the centre of the circle. OL and OM are perpendiculars from O to the chords AB and CD respectively. If OL=OM and AB=16cm, then find the length of CD.
 View Solution
View SolutionIn the given figure O is the centre of the circle and AB is a tangents at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of the circle.
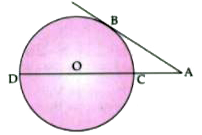 View Solution
View SolutionChords AB and CD of a circle when extended meet at point X. Given AB =4 cm, BX=6 cm and XD=6cm, calculate the length of CD.
View SolutionIn the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD
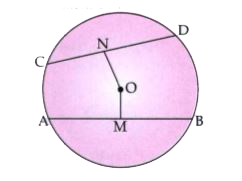 View Solution
View Solution

