O is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
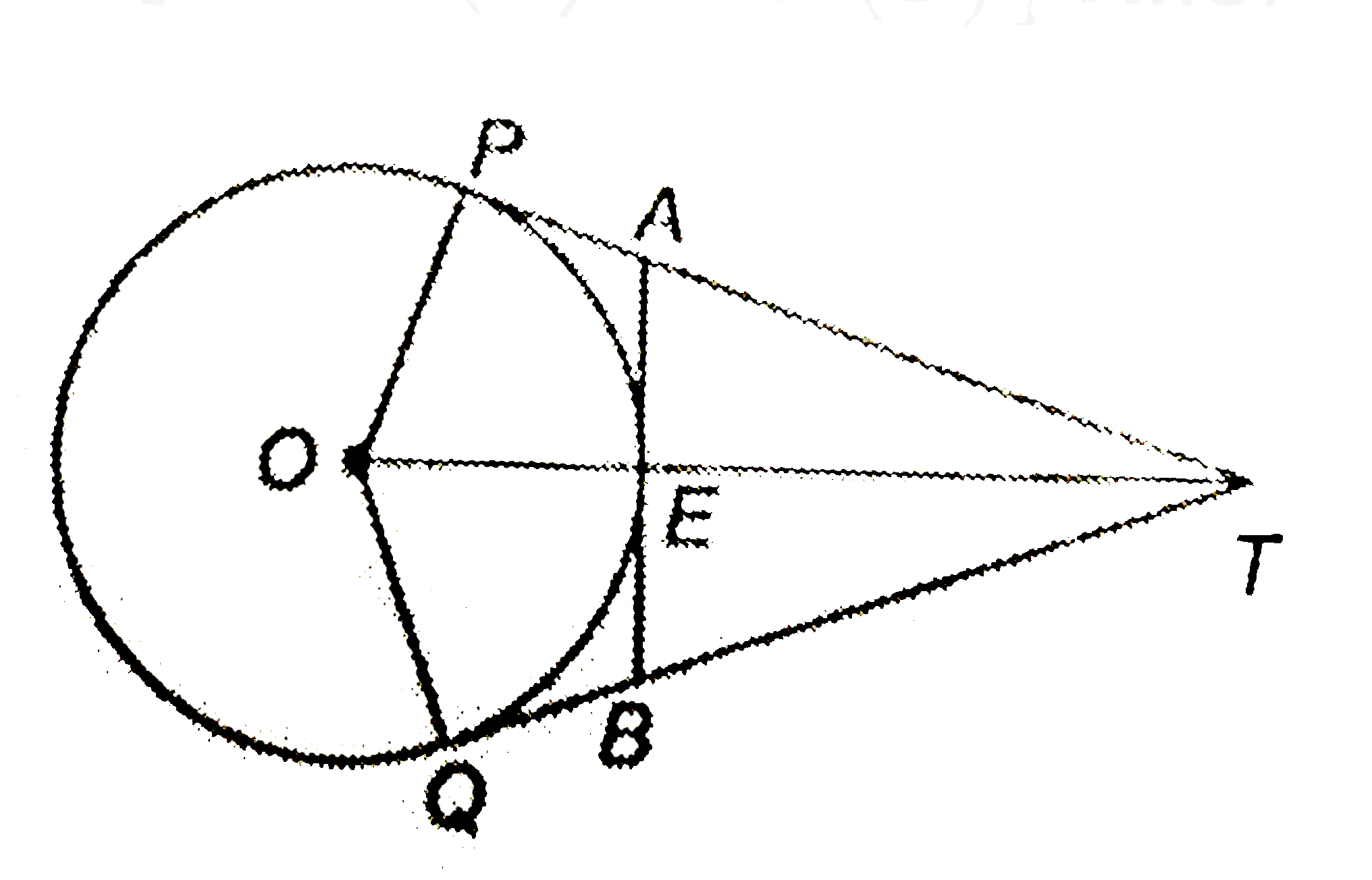
Since, ∠OPT=90∘
(radius through point of contact is ⊥ to the tangent)
∴ In right △OPT,
OP2+PT2=OT2 (by Pythagoras theorem)
⇒ PT2=OT2−OP2
⇒ PT2=(13)2−(5)2=(12)2
⇒ PT=12cm
LetAP=xcm
∴ AE=AP=x (lengths of tangents from an external point are equal)
∴ AT=TP−AP=12−x
ET=OT−OE=13−5=8cm
Now, since ∠AEO=90∘ (radius through point of contact is ⊥ to the tangent)
∴ ∠AET=90∘ (L.P.A)
∴ In right △AET, by Pythagoras theorem,
AE2+ET2=AT2
Circles
⇒ x2+(8)2=(12−x)2
⇒ x2+64=144+x2−24x
⇒ 24x=144−64=80
⇒ x=8024=103
Similarly, BE=103cm
∴ AB=AE+BE=(103+103)cm=203cm
Hence, AB=203cm
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar11videos
CIRCLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise32videos
CIRCLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question5videos
ARITHMETIC PROGRESSION
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions10videos
CO-ORDINATE GEOMETRY
Similar Questions
O is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find length of AB.
View SolutionType V: O is the center of the circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E . If AB is the tangent to the circle at E; find the length of AB.
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
View SolutionAB is a chord of length 16cm of a circle of radius 10cm. The tangents at A and B intersect at a point P . Find the length of PA .
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see Fig. 10.10). Find the length TP.
View SolutionIn a circle of radius 7 cm, tangent PT is drawn from a point P such tht PT= 24 cm. If O is the centre of circle, then find the length of OP.
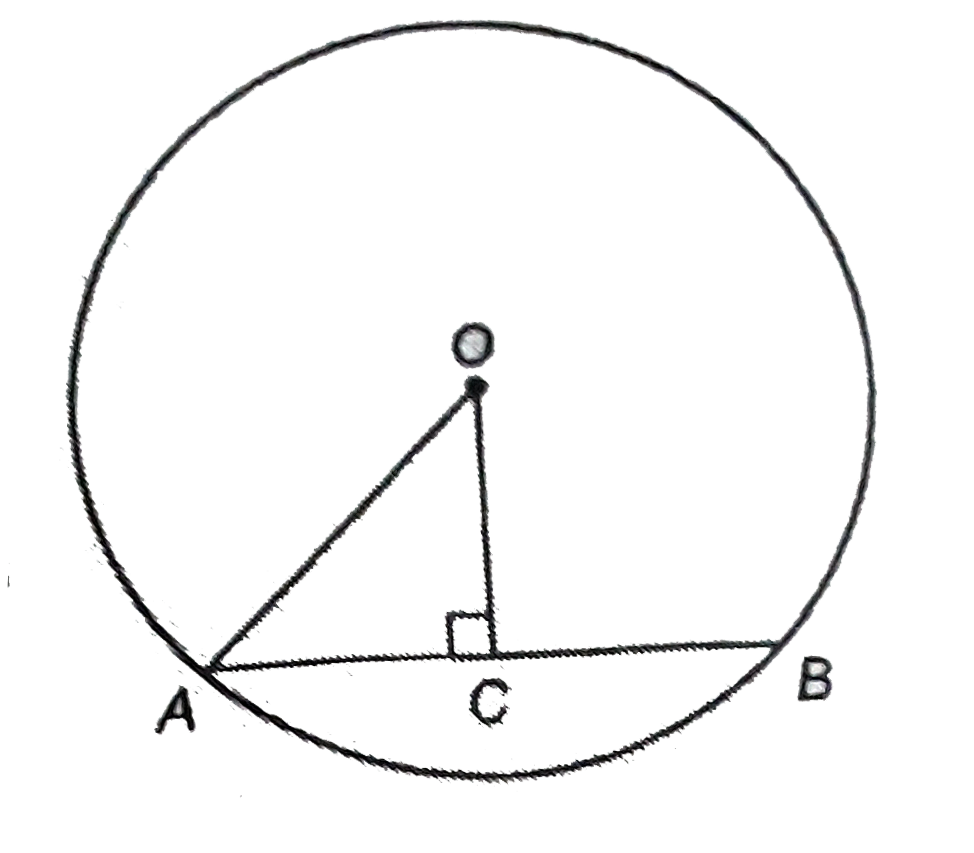
View SolutionIn the adjoining figure O is the centre of circle and c is the mid point. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
 View Solution
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ=13cm . Find the length of PQ .
View SolutionA is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ΔABC
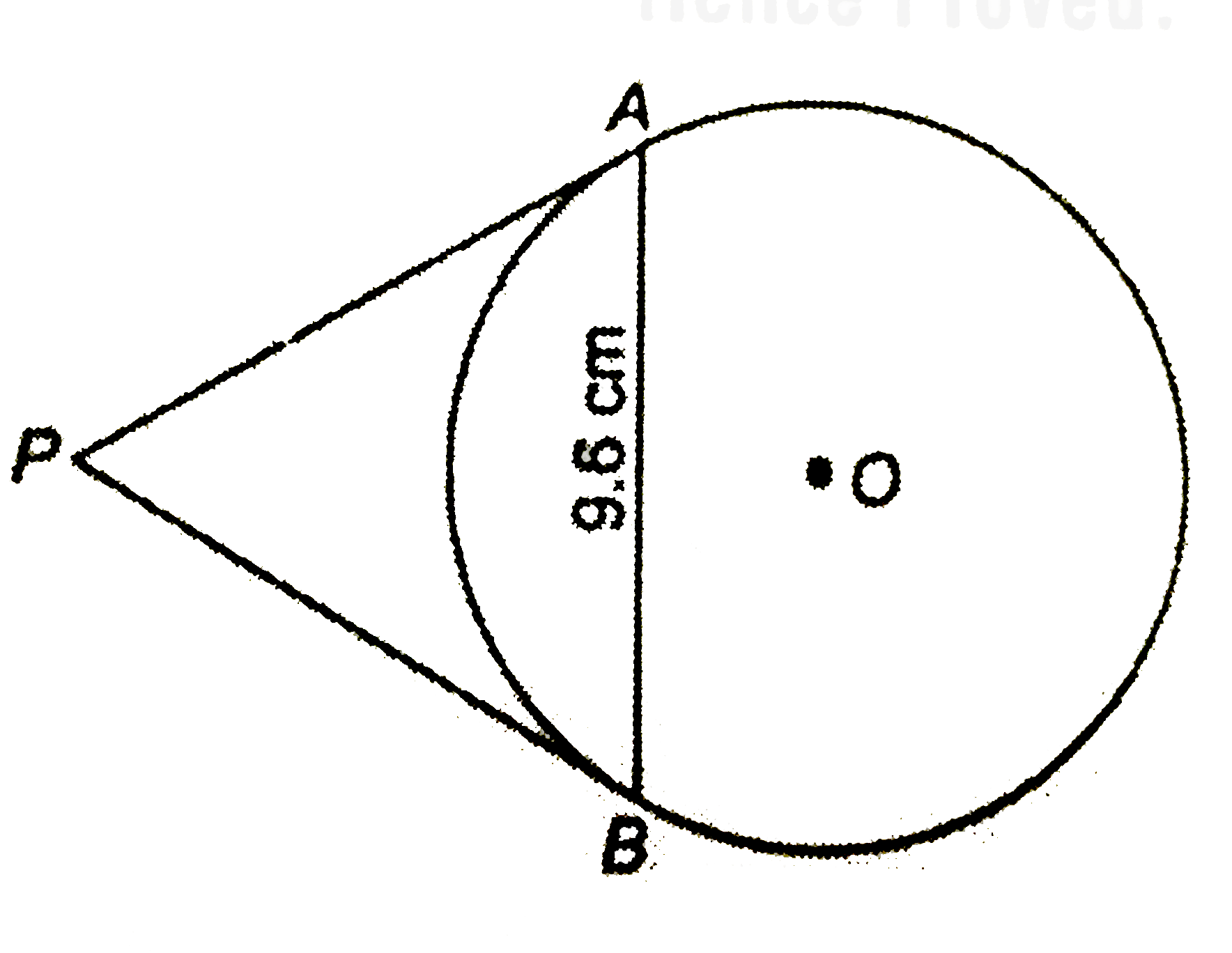
View SolutionIn the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
 View Solution
View Solution

