Draw the graph of following functions.
f(x)=|x|+|x−1|
The correct Answer is:=−2x+1
To draw the graph of the function f(x)=|x|+|x−1|, we will analyze the function by breaking it down into intervals based on the points where the expressions inside the absolute values change sign.
Step 1: Identify critical points
The critical points occur when the expressions inside the absolute values are zero:
1. |x|=0 at x=0
2. |x−1|=0 at x=1
This gives us the critical points x=0 and x=1. We will analyze the function in three intervals:
- (−∞,0)
- (0,1)
- (1,∞)
Step 2: Analyze the intervals
Interval 1: x<0
In this interval, both x and x−1 are negative:
- |x|=−x
- |x−1|=−(x−1)=−x+1
Thus, the function becomes:
f(x)=−x+(−x+1)=−2x+1
Interval 2: 0≤x<1
In this interval, x is non-negative and x−1 is negative:
- |x|=x
- |x−1|=−(x−1)=−x+1
Thus, the function becomes:
f(x)=x+(−x+1)=1
Interval 3: x≥1
In this interval, both x and x−1 are non-negative:
- |x|=x
- |x−1|=x−1
Thus, the function becomes:
f(x)=x+(x−1)=2x−1
Step 3: Combine the results
Now we have the piecewise function:
f(x)=⎧⎨⎩−2x+1if x<01if 0≤x<12x−1if x≥1
Step 4: Plot the graph
1. For x<0: The line f(x)=−2x+1 has a y-intercept at (0,1) and a slope of -2. It will decrease as x decreases.
2. For 0≤x<1: The function is constant at f(x)=1.
3. For x≥1: The line f(x)=2x−1 has a y-intercept at (0,−1) and a slope of 2. It will increase as x increases.
Step 5: Mark critical points and draw the graph
- At x=0, f(0)=1.
- At x=1, f(1)=1.
Now, we can sketch the graph:
- Start from the left, drawing the line f(x)=−2x+1 until x=0.
- From x=0 to x=1, draw a horizontal line at y=1.
- From x=1 onward, draw the line f(x)=2x−1.
Final Graph
The graph consists of:
- A decreasing line from (0,1) to (−∞,1).
- A horizontal line from (0,1) to (1,1).
- An increasing line from (1,1) onward.
The critical points occur when the expressions inside the absolute values are zero:
1. |x|=0 at x=0
2. |x−1|=0 at x=1
- (−∞,0)
- (0,1)
- (1,∞)
In this interval, both x and x−1 are negative:
- |x|=−x
- |x−1|=−(x−1)=−x+1
f(x)=−x+(−x+1)=−2x+1
In this interval, x is non-negative and x−1 is negative:
- |x|=x
- |x−1|=−(x−1)=−x+1
f(x)=x+(−x+1)=1
In this interval, both x and x−1 are non-negative:
- |x|=x
- |x−1|=x−1
f(x)=x+(x−1)=2x−1
Now we have the piecewise function:
f(x)=⎧⎨⎩−2x+1if x<01if 0≤x<12x−1if x≥1
1. For x<0: The line f(x)=−2x+1 has a y-intercept at (0,1) and a slope of -2. It will decrease as x decreases.
2. For 0≤x<1: The function is constant at f(x)=1.
3. For x≥1: The line f(x)=2x−1 has a y-intercept at (0,−1) and a slope of 2. It will increase as x increases.
- At x=0, f(0)=1.
- At x=1, f(1)=1.
- Start from the left, drawing the line f(x)=−2x+1 until x=0.
- From x=0 to x=1, draw a horizontal line at y=1.
- From x=1 onward, draw the line f(x)=2x−1.
The graph consists of:
- A decreasing line from (0,1) to (−∞,1).
- A horizontal line from (0,1) to (1,1).
- An increasing line from (1,1) onward.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2 (a)24videos
RELATIONS AND FUNCTIONS
- BOOK - ICSECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2 (b)26videos
RELATIONS AND FUNCTIONS
- BOOK - ICSECHAPTER - RELATION AND FUNCTIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (Choose the correct answer from the given four options in questions)32videos
RELATION AND FUNCTIONS
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 01EXERCISE - SECTION C8videos
SAMPLE QUESTION PAPER 01
Similar Questions
Draw the graph of following functions.
f(x)=|x|xView SolutionDraw the graph of the following function.
2f(x)View SolutionDraw the graph of the following function.
−f(x)View SolutionDraw the graph of the following function.
f(−x)View SolutionDraw the graph of the following function.
f(x+1)View SolutionConsider the following function f whose graph is given below.
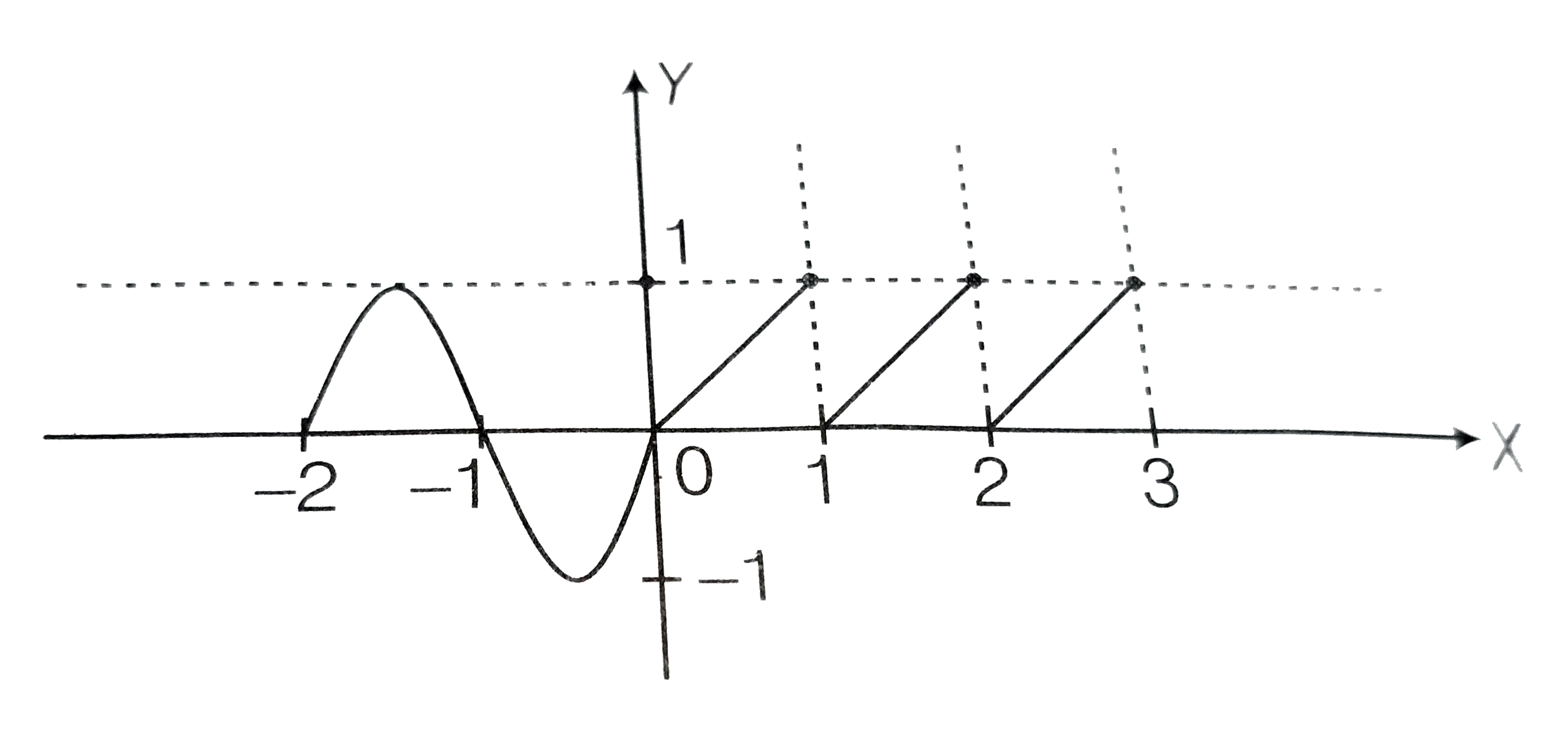
Draw the graph of following functions.
f(x)−1View SolutionDraw the graph of the following function.
12f(x)View SolutionConsider the following function f whose graph is given below.
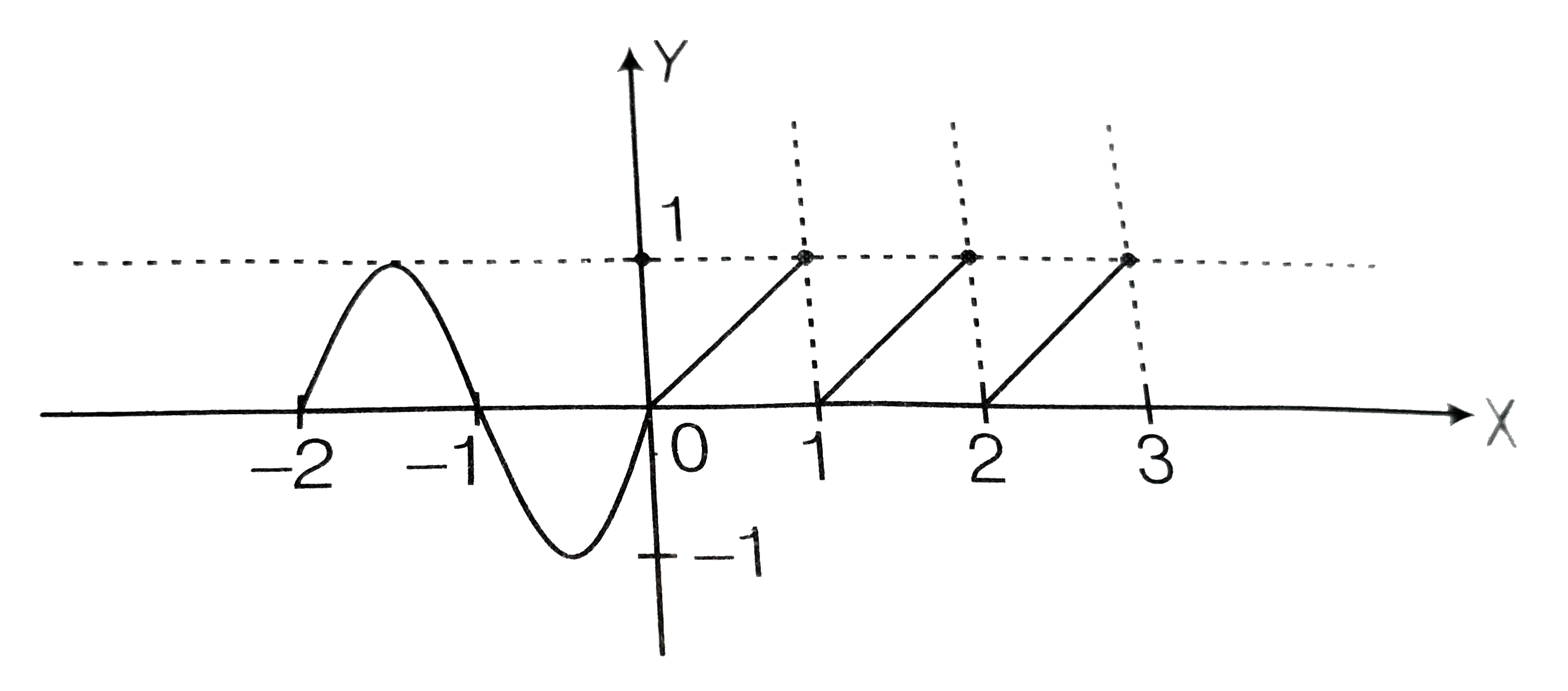
Draw the graph of following functions.
(a) f(x)+1View SolutionConsider the following function f whose graph is given below.

Draw the graph of following functions.
(f) f(|x|)View SolutionConsider the following function f whose graph is given below.

Draw the graph of following functions.
f(2x)View Solution

