Question

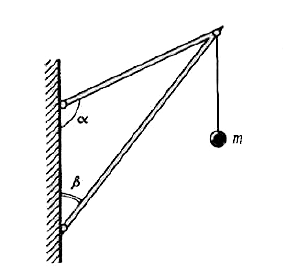
A weight of mass m hangs from a bracket (Fig.),
AB = AC = BC = EC = a, DE = a/2. Find the forces in the rods.

Answer

mg, mg and 2 mg

Explanation

Since `DC = a sqrt(3//2) and DE = a//2` it follows that `angleCDE = 90^(@)`. Resolve the force P = mg into two components in the directions CD and CE (Fig.). We obtain N = 2P, `F= P sqrt(3)`. Now resolve


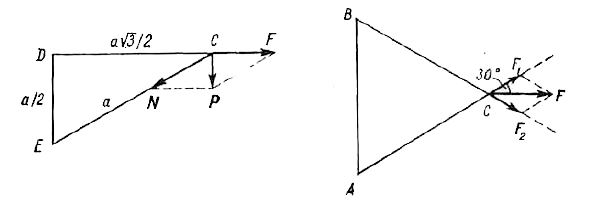
the force F into components directed along the rods BC and AC (Fig.). Since in this case the parallelogram of forces is a rhombus with an apex angle of `60^(@)`, it follows that
`F_(1)=F_(2) = (F)/(2 cos 30^(@)) = (P sqrt(3))/(2 sqrt(3//2)) =P`