Question

A charge q is uniformly distributed over the surface of a ring-shaped conductor of radius a. Find the field intensity on the axis of the conductor at a distance x from the plane of the conductor.

Answer

`E=(qx)/(4pi epsilon_(0)(a^(2)+x^(2))^(3//2))`

Explanation

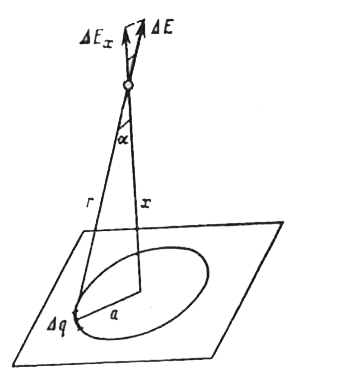
Divide the conductor into segments of such small length that they may be considered to be point (Fig. ). Then the projection of the field intensity set up by a small segment on the axis of symmetry of the conductor will be
`DeltaE_(x)= (Delta q cos alpha)/(4 pi epsilon_(0)r^(2)) = (Deltaq*x)/(4pi epsilon_(0) r^(3))= (Delta q*x)/(4pi epsilon_(0) (a^(2) +x^(3))^(3//2))`
From considerations of symmetry it is evident that the field is directed along the axis and tht the field intensity is the sum of the projections of the field intensities set up by the individual segments of the conductor.