An electric field of intensity E is set up between two parallel plates of length L. An electron beam enters the field at an angle α>0 to the plates and leaves it at an angle β<0 (Fig.). Find the initial velocity of the electrons. The force of gravity is to be neglected.
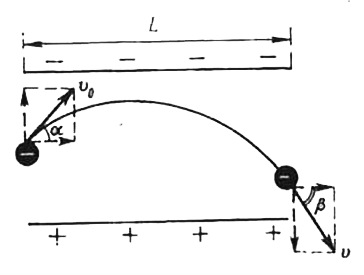
The correct Answer is:v0=√eELcosβmcosαsin(α−β)
Since there are no forces in the direction of the x-axis acting on the electron (we neglect the force of gravity), vx= const, and the electron transit time in the field is t=L/vx. The force acting on the electron in the direction of the y-axis is Fy=−eE. This force imparts to the electron an acceleration ay=−eE/m. The projection of the velocity on the y-axis varies with time according to the equation vy=v0y+ayt. At the point of the electron.s exist from the field we have
vxtanβ=vxtanα−eELmvx, from which v2x(tanα−tanβ)=eELm
Since vx=v0cosα, we obtain
v20cos2α(tanα−tanβ)=eEL/m
Similar Questions
The length of plane-parallel electrodes is l, the distance between them is h. An electric field of intensity E is set up between them. An electron enters the field close to the lower plate at an initial speed v0 and at an angle α to the plates (Fig.). What should the field intensity be for the electron to pass between the electrodes without striking either of them? For what angles α is this possible?
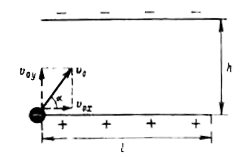
View SolutionA uniform electric field E is created between two parallel
., charged plates as shown in figure . An electron
. enters the field symmetrically between the plates with a
. speed v_(0)'. The length of each plate is l. Find the angle of
. deviation of the path of the electron as it comes out
. of the field.
View Solution
Knowledge Check
A uniform electric field E is created between two parallel charged plates as shown in figure . An electron enters the field symmetrically between the plates with a speed v0. The length of each plate is l. Find the angle of deviation of the path of the electron as it comes out of the field.
Aθ=tan−1(el)mv20Bθ=tan−1(eEl)v20Cθ=tan−1(eEl)mv20Dθ=tan−1(eEl)v20v33.2
A0.34 mmnB0.57 mmC7.5 mmD0.75 mm
A uniform electric field E is created between two parallel
., charged plates as shown in figure . An electron
. enters the field symmetrically between the plataes with a
. speed v_0. The length of each plate is l. Find the angle of
. deviation of the path of the electron as it comes out
. of the field.
View SolutionA uniform electric field E is created between two parallel
., charged plates as shown in figure . An electron
. enters the field symmetrically between the plataes with a
. speed v_0. The length of each plate is l. Find the angle of
. deviation of the path of the electron as it comes out
. of the field.
θ
=
tan
−
1
E
l
m
v
2
0
θ
=
tan
−
1
(
e
E
l
m
v
2
0
)
θ
=
tan
−
1
(
e
E
l
m
v
0
)
θ
=
tan
−
1
(
e
E
m
v
2
0
)
View SolutionIF an electron enters into a space between the plates of a parallel plate capacitor at an an angle α with the plates an leaves at an angle β to the plates find the ratio of its kinetic energy while entering the capacitor of that while leaving.
View SolutionIF an electorn enters into a space between the plates of a parallel plate capacitor at an an angle α with the plates an leaves at an angle β to the plates find the ratio of its kinetic energy while entering the capacitor of that while leaving.
View SolutionA uniform electric field E is established between two parallel charged plates as shown in figure. An electron enter the field symmetrically between the plates with a speed u. The length of each plate is l. if the electron does not stricke any of the plates, find the angle of deviation of the electron as it comes out of the field at the outer end of plates. [tan−1(eElμ2)]
View Solution[" 0.A electric field of "1.5times10^(4)NC^(-1)" exists "],[" between two parallel plates of length "2cm." An "],[" electron enters the region between the plates "],[" at right angles to the field with a kinetic energy "],[" of "E_(k)=2000eV." The deflection that the "],[" electron experiences at the deflecting plates "],[" is "]
View Solution