The length of plane-parallel electrodes is l, the distance between them is h. An electric field of intensity E is set up between them. An electron enters the field close to the lower plate at an initial speed v0 and at an angle α to the plates (Fig.). What should the field intensity be for the electron to pass between the electrodes without striking either of them? For what angles α is this possible?
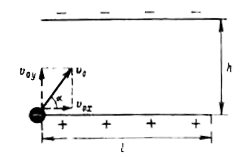
The correct Answer is:0<tanα<4hl;mv20sin2α2eh<E<mv20sin2αel.
No forces act on the electron in the x-direction and it moves along this axis at a constant speed vx=v0cosα. In the y-direction a force Fy=−eE acts on the electron, and it moves with an acceleration ay=−eE/m, its instantaneous velocity is
vy=v0sinα+ayt=v0sinαu−eEtm
To prevent the electron moving upwards from striking the upper plate, a field has to be established that would in time t1 reduce the vertical velocity component to zero and would guarantee the condition h1<h. But 2ayh1=−v20y
therefore
∣∣ay∣∣=v20y2h1>v20sin2α2h
Hence, the first condition may be written in the form
E>=mv20sin2α2eh
The time the electron moves upwards is t1=−v0sinαay The time it moves downwards will be the same (prove this!). To prevent it form striking the lower plate it must be made to travel during this time a distance in the x-direction exceeding the length of the plate, i.e. x=2vxt1>l. Hence
−2v20sinαcosαay>l
and the second condition assumes the form
E<2mv20sinαcosαel
Combining both solutions we obtain the result sought.
Similar Questions
दो आवेशित प्लेटों के बीच विद्युत् क्षेत्र की तीव्रता 10 वोल्ट/मीटर है। यदि इनके बीच परावैद्युत माध्यम भर दिया जाता है तो विद्युत् क्षेत्र की तीव्रता घटकर 2.5 वोल्ट/मीटर रह जाती है। माध्यम का परावैद्युतांक क्या है ?
View SolutionWhat is the electric field intensity between the plates of a capacitor?
View Solution
दोनों प्लेटो के बीच में विधुत क्षेत्र की तीव्रता का मान होगा
View SolutionA uniform electric field E is created between two parallel
., charged plates as shown in figure . An electron
. enters the field symmetrically between the plataes with a
. speed v_0. The length of each plate is l. Find the angle of
. deviation of the path of the electron as it comes out
. of the field.

View SolutionA uniform electric field E is created between two parallel
., charged plates as shown in figure . An electron
. enters the field symmetrically between the plates with a
. speed v_(0)'. The length of each plate is l. Find the angle of
. deviation of the path of the electron as it comes out
. of the field.

View SolutionAn electric field of intensity E is set up between two parallel plates of length L. An electron beam enters the field at an angle α>0 to the plates and leaves it at an angle β<0 (Fig.). Find the initial velocity of the electrons. The force of gravity is to be neglected.
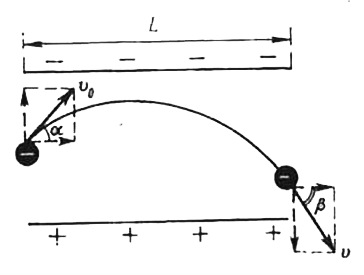
View SolutionTwo plane-parallel plates l=2cm long serve as the control electrodes of a cathode-ray tube. The distance from the control electrodes to the tube's screen is L = 30 cm. An electron beam enters midway between the plates parallel to them at a velocity of v0=2×107m/s. What is the electric field between the electrodes if the beam's displacement on the screen is d=12cm?
View Solution
