Find the center of mass of a plate shown in Fig. 7 .11. Put R = 5.00 cm, r = 3.00 cm.

The correct Answer is:At a distance of x=r2R+r=1.13 cm to the left of the centre of the large circle.
Similar Questions
Knowledge Check
What mass of water (at 4.0∘C) can be contained in a rectangular box whose dimensions are 10.0 cm by 5.00 cm by 1.00 cm? The density of water at 4.0∘C is 1000kg/m3.
A5.0 gB10.0 gC25.0 gD50.0 g
A circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View SolutionThe variation of potential with distance r from a fixed point is shown in fig. The electric field at r = 5cm, is :

View SolutionThe variation of potential with distance r from a fixed point is shown in fig. The electric field at r = 5cm, is :

View SolutionA nonconducting sphere of radius R=5cm has its center at the origin O of the coordinate system as shown in (Fig. 3.112). It has two spherical cavities of radius r=1cm, whose centers are at 0,3cm and 0,−3cm, respectively, and solid material of the sphere has uniform positive charge density ρ=1/πμCm−3. Calculate the electric potential at point P(4cm,0).
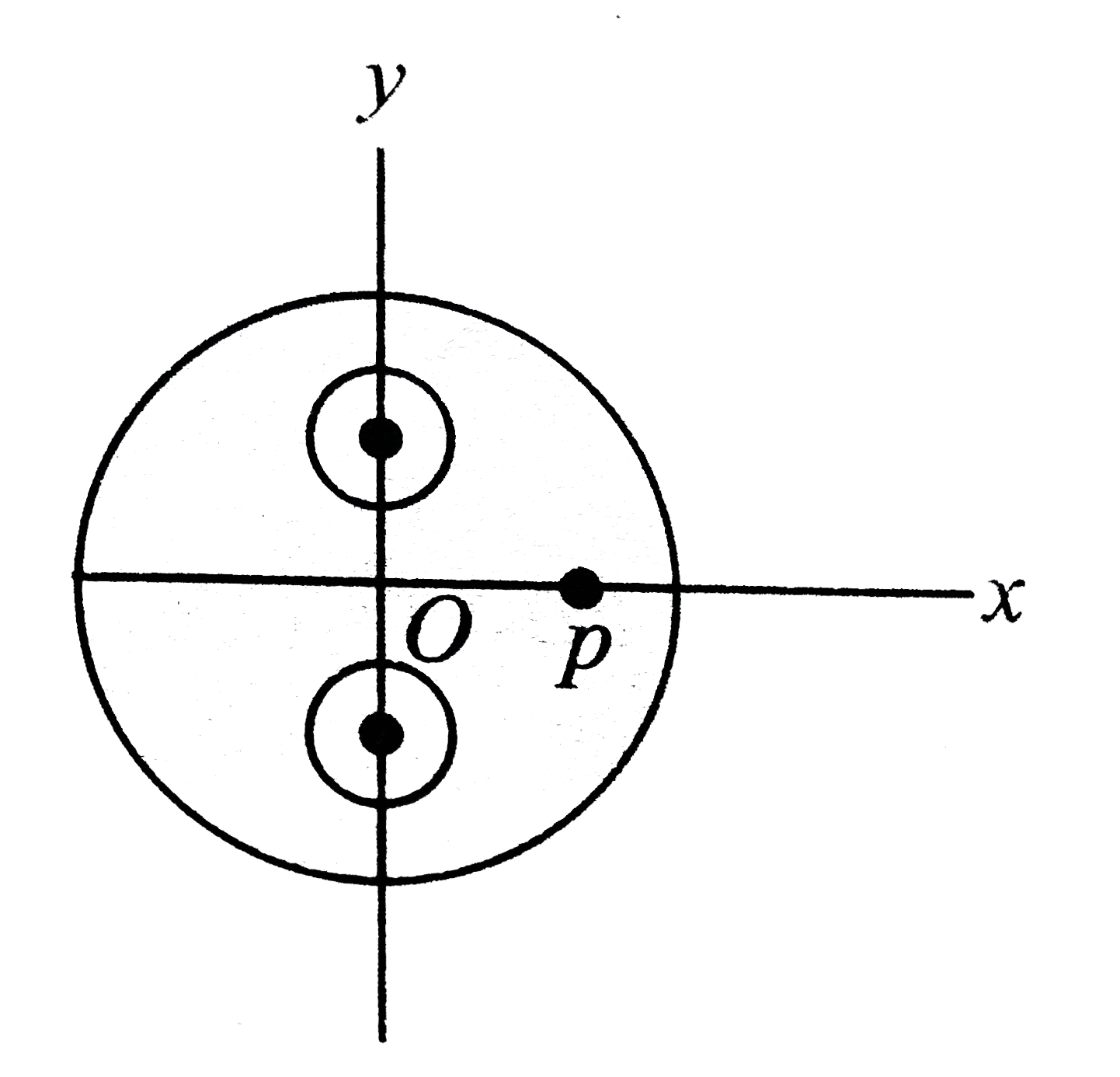 .
.
View SolutionA nonconducting sphere of radius R=5cm has its center at the origin O of the coordinate system as shown in (Fig. 3.112). It has two spherical cavities of radius r=1cm, whose centers are at 0,3cm and 0,−3cm, respectively, and solid material of the sphere has uniform positive charge density ρ=1/πμCm−3. Calculate the electric potential at point P(4cm,0).
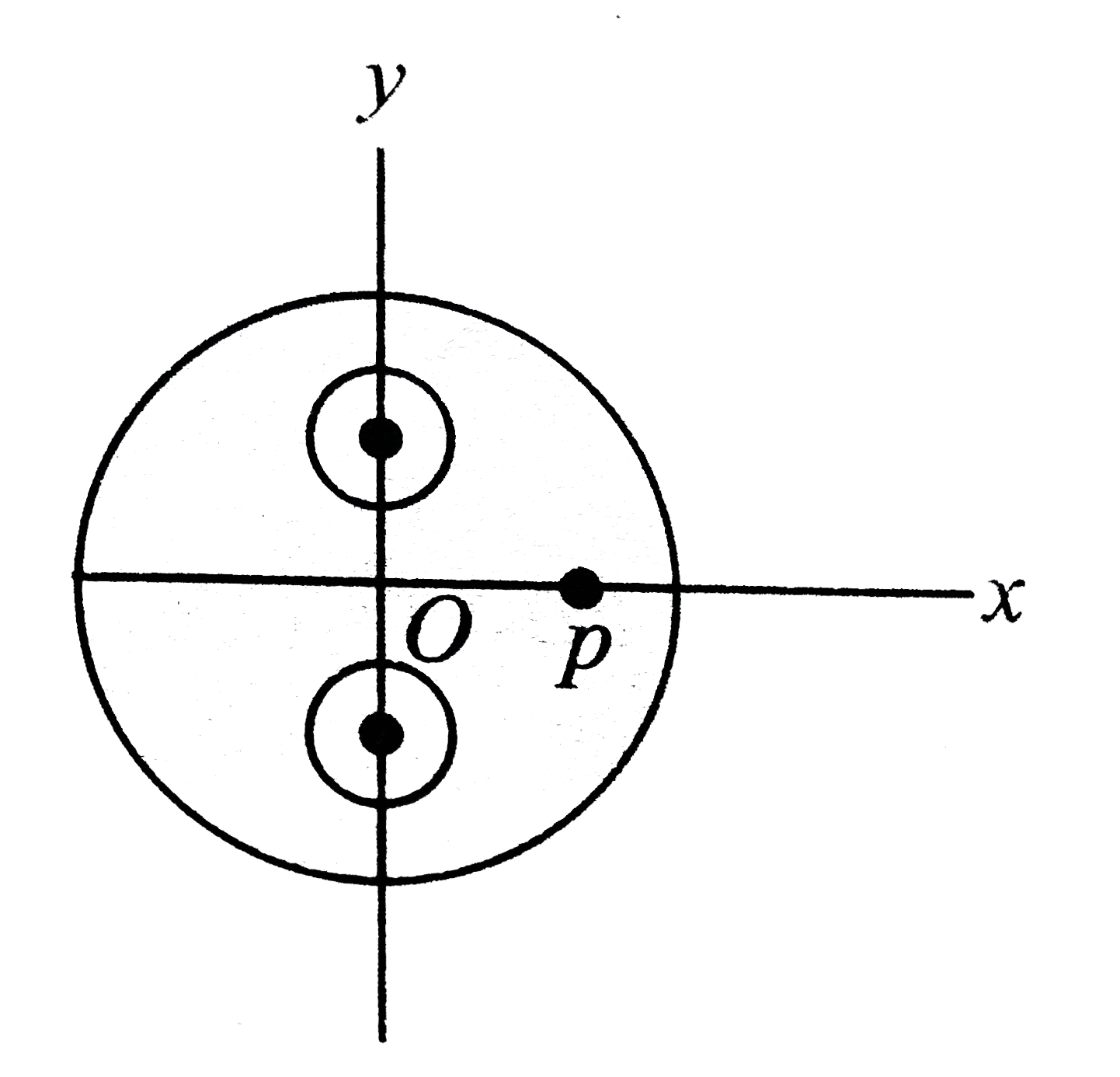 .
.
View SolutionIn Fig.(i), a lens of focal length 10cm is shown. It is cut into two parts and placed as shown in Fig.(ii). An object AB of light 1cm is placed at a distance of 7.5cm. The height of the image will be

View SolutionThe gas between two long coaxial cylindrical surfaces is filled with a homogeneous isotropic substance. The radii of the surfaces are r1=5.00cm and r2=7.00cm. In the steady state the temperatures of the inner and outer surfaces are T1=290Kand=320K respectively. Find the temperature of a coaxial surface of radius r.
View Solution