Using numerical methods find the center of mass of a semicircle. To facilitate computation put R = 1.00.
Divide the radius into 10 equal parts and find the coordinates of the centres of mass of the strips (see Fig. 7.12). All of them lie on Lhe x-axis, their coordinates being shown in the sec- ond column of Table 7 .12. Since we assume the plate lo be uniform, the mass of each strip is proportional to its area, i.e.

Mn∝Sn2Δxrn
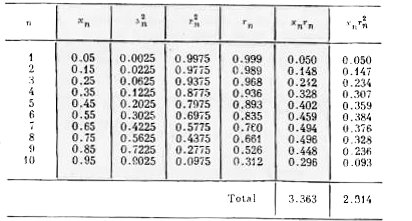
where Δx=0.1. Now the product of the segments.of a chord is equal to the ·product of the 5egments of the diameter, i.e.
r2n=(1−xn)(1+xn)=1−x2n
To determine the position of the centre of mass compute
xc=S1x1+S2x2+.....+S10x10S1+S2+......+S10
=2Δx(r1x1+r2x2+.....+r10x10)π/2=0.4×3.363π=0.428
Hence, the coordinate of the centre of inertia of a semicircle is Xc==0.428R.
Similar Questions
Using numerical methods find the center of mass of a hemisphere .
View SolutionUsing numerical methods find the center of mass of a right circular cone with the height h = 1 and its generatrix making an angle with the height.
View SolutionUsing the first Guldin theorem, find the centre of gravity of a semicircle of radius a.
View SolutionFind the center of mass of a plate shown in Fig. 7 .11. Put R = 5.00 cm, r = 3.00 cm.

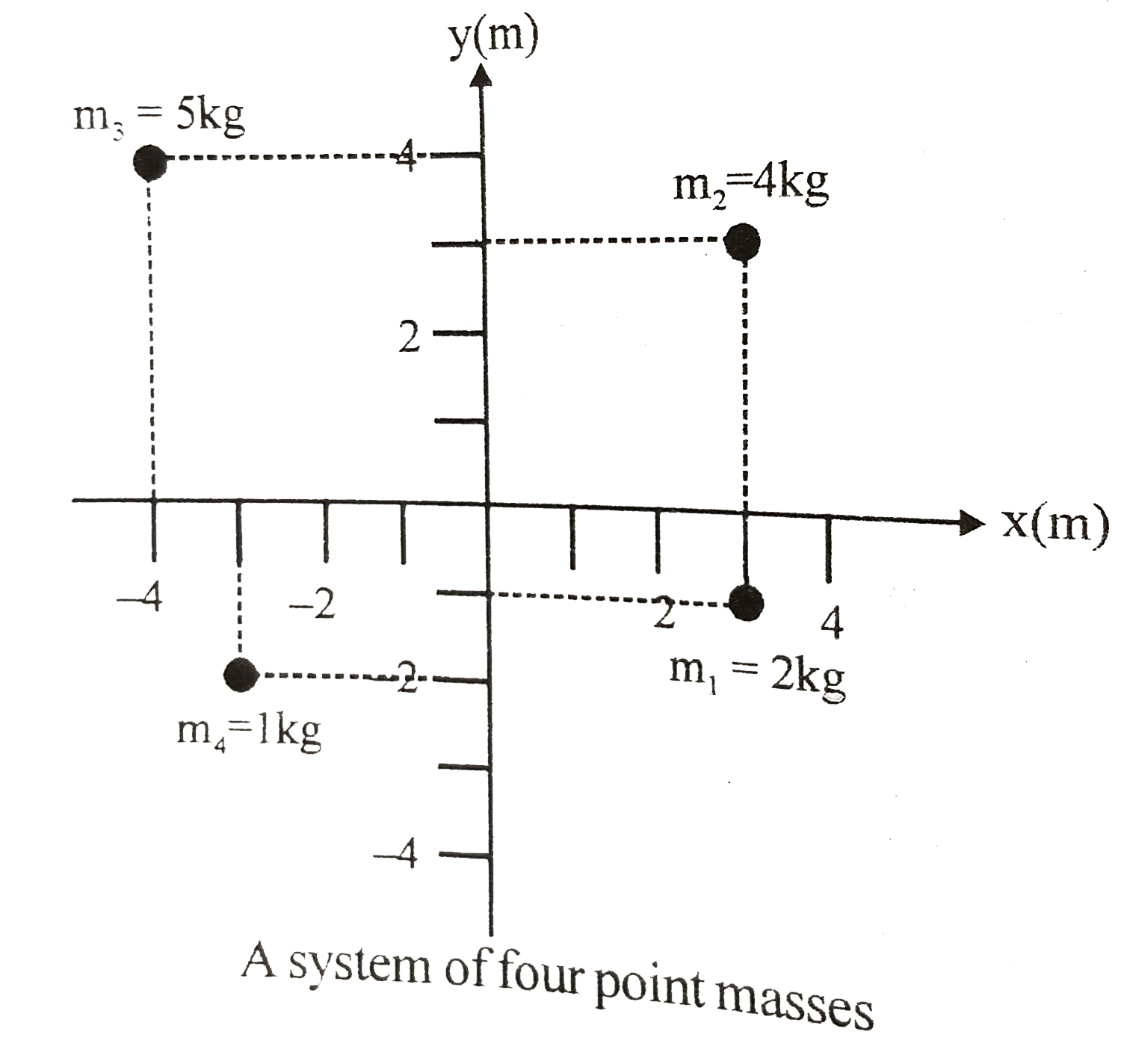
View SolutionFind the center of mass of the four point masses as shown in figure.
View SolutionFind the centre of gravity of a thin wire bent to a semicircle of radius r.
View SolutionFind the velocity of the center of mass of the system shown in the figure .

View SolutionFind the velocity of center of mass of the system shown in the figure.

View SolutionFind the velocity of center of mass of the system shown in the figure.

View SolutionUse the tables and find the cube root of 1.00456.
View Solution
