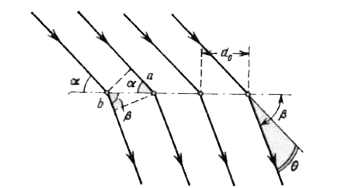
A plane wave falls on a diffraction grating with a grating constant $d_{0}$ at a glancing angle $α$ . Prove that the resulting diffraction will be the same as when the wave falls normally on a grating with a grating constant of d = $d_{0} sin α$ .

Text Solution

Verified by Experts

Let a paralle heam. That is a plane wave, fall on the grating at a glaneing angle of $α$ (Fig. 40.14). The direction of the zero - order interference maximum will obviously be the same. As to the maximum of order m, its direction will be at a glancing angle $β$ , so that the propagation difference is $Δ a - b = m λ$ . Noting that $a = d_{0} cos α, b = d_{0} cos β$ , where $d_{0}$ is the grating constant, we obtain
$d_{0} (cos α - cos β) = m λ$
This is just the condition for the interference maxima when the light rays are incident at an angle to the diffraction grating. Now let us express the interference condition for the angle $θ$ equal to the deflection angle of the diffraction maximum from the original direction of the beam. Since $β = α + θ$ , it follows that
$cos α - cos β = cos α - cos (α + θ) = cos α - cos α θ + sin α sin θ$
Since the angle $θ$ is usually very small, $cos θ \approx 1$ , and $cos α - cos β \approx sin α sin θ$ . The condition for the maximum assume the from
$d_{0} sin α sin θ = m λ$
i.e. the instrument behaves with respect to the inclined beam in the way it would have done if a grating with constant $d = d_{0} sin α$ were placed perpendicular to the rays.

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile