Intensity of electric field at a perpendicular distance of 0.5 m from an infinitely long line charge having linear charge density (λ) is 3.6×103Vm−1 . Find the value of λ
To find the value of the linear charge density λ for an infinitely long line charge, we can use the formula for the electric field E at a perpendicular distance R from the line charge:
E=λ2πϵ0R
Where:
- E is the electric field intensity,
- λ is the linear charge density,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2,
- R is the distance from the line charge.
Step 1: Rearranging the formula
We need to rearrange the formula to solve for λ:
λ=E⋅2πϵ0R
Step 2: Substituting the known values
Given:
- E=3.6×103V/m
- R=0.5m
- ϵ0=8.85×10−12C2/N m2
Now substituting these values into the rearranged formula:
λ=(3.6×103)⋅(2π)⋅(8.85×10−12)⋅(0.5)
Step 3: Calculating the value
Calculating each component step-by-step:
1. Calculate 2π:
2π≈6.2832
2. Now calculate 2π⋅ϵ0:
2π⋅(8.85×10−12)≈6.2832⋅8.85×10−12≈5.570×10−11
3. Now multiply by R:
5.570×10−11⋅0.5≈2.785×10−11
4. Finally, multiply by E:
λ=(3.6×103)⋅(2.785×10−11)≈1.000×10−7C/m
Final Answer
Thus, the value of λ is:
λ≈1.0×10−7C/m
---
- E is the electric field intensity,
- λ is the linear charge density,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2,
- R is the distance from the line charge.
We need to rearrange the formula to solve for λ:
Given:
- E=3.6×103V/m
- R=0.5m
- ϵ0=8.85×10−12C2/N m2
Calculating each component step-by-step:
2π≈6.2832
2π⋅(8.85×10−12)≈6.2832⋅8.85×10−12≈5.570×10−11
5.570×10−11⋅0.5≈2.785×10−11
λ=(3.6×103)⋅(2.785×10−11)≈1.000×10−7C/m
Thus, the value of λ is:
Similar Questions
Intensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
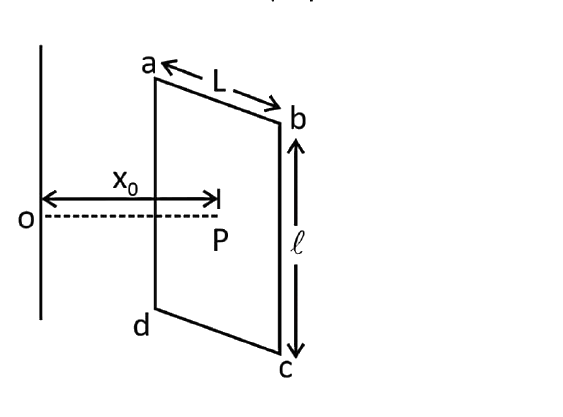
View SolutionFind the electric flux (in S.I. unit) through the rectangular plate abcd of length l=2m width L and whose centre is at a distance OP=x0=L2 from an infinite line of charge with linear charge density λ=136π×10−9Cm−1. Consider that the plate of the frame is perpendicular to line OP.
View SolutionElectric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
View SolutionThe electric field due to a point charge at a distance 6 m from it is 630 N/C. The magnitude of the charge is
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View SolutionLet E1(r), E2(r) and E3(r) be the respectively electric field at a distance r from a point charge Q, an infinitely long wire with constant linear charge density λ, and an infinite plane with uniform surface charge density σ. If E1(r0)=E2(r0)=E3(r0) at a given distance r0, then
View SolutionFind the electric flux crossing the wire frame ABCD of length l, width b, and center at a distance OP = d from an infinite line of charge with linear charge density λ. Consider that the plane of the frame is perpendicular to the line OP

View SolutionAn electric dipole consists of charges ±2.0×10−8 C separated by distance of ±2.0×10−3m. It is placed at a distance of 6 cm from a line charge of linear charge density 4.0×10−4Cm−1 as shown in figure such that the dipole makes an angle of θ=60∘ with line AB. Find the force acting on the dipole.

View Solution
