If R1andR2 are filament resistances of a 200 W and a 100 W bulb respectively, designed to operate on the same voltage, then :
R1=R2
R2=2R1
R2=4R1
R1=4R2
The correct Answer is:B
To solve the problem, we will use the relationship between power, voltage, and resistance. The power P of an electrical device can be expressed in terms of voltage V and resistance R using the formula:
P=V2R
Step 1: Write down the power formulas for both bulbs.
For the 200 W bulb (let's denote its resistance as R1):
P1=V2R1(1)
For the 100 W bulb (let's denote its resistance as R2):
P2=V2R2(2)
Step 2: Rearrange the formulas to express resistance in terms of power.
From equation (1), we can express R1:
R1=V2P1(3)
From equation (2), we can express R2:
R2=V2P2(4)
Step 3: Substitute the power values into the resistance equations.
Substituting P1=200 W and P2=100 W into equations (3) and (4):
R1=V2200(5)
R2=V2100(6)
Step 4: Find the relationship between R1 and R2.
Now, we can find the ratio of R2 to R1:
R2R1=V2100V2200=200100=2
This implies:
R2=2R1(7)
Conclusion
Thus, the relationship between the resistances is:
R2=2R1
Final Answer
The correct option is that R2 is equal to 2R1.
---
For the 200 W bulb (let's denote its resistance as R1):
P1=V2R1(1)
For the 100 W bulb (let's denote its resistance as R2):
P2=V2R2(2)
From equation (1), we can express R1:
R1=V2P1(3)
From equation (2), we can express R2:
R2=V2P2(4)
Substituting P1=200 W and P2=100 W into equations (3) and (4):
R1=V2200(5)
R2=V2100(6)
Now, we can find the ratio of R2 to R1:
R2R1=V2100V2200=200100=2
This implies:
R2=2R1(7)
Thus, the relationship between the resistances is:
R2=2R1
The correct option is that R2 is equal to 2R1.
Similar Questions
If R1 and R2 are respectively the filament resistances of a 200 watt bulb and 100 watt bulb designed to operate on the same voltage, then
View SolutionIf R1 and R2 are the resistances of the filaments of 200 W and 100 W electric bulbs operated at 220 V, then (R1R2) is
View SolutionIncandescent bulbs are designed by keeping in mind that the resistance of their filament increases with the increase in temperature. If at room temperature, 100W,60Wand40W bulbs have filament resistances R100,R60andR40, respectively, the relation between these resistances is
View SolutionIn the circuit shown in figure-3.391, V1andV2 are two voltmeters having resistances 6000Ωand4000Ω respectively EMF of battery is 250V, having negligible internal resistance. Two resistances R1andR2 are 4000Ωand6000Ω respectively. Find the reading of the voltamter V1andV2 when
(a) Switch S is open ltbgt (b) Switch S is closed
 View Solution
View SolutionIn the figure shown B1,B2 and B3 are three bulbs rated as (200V, 50 W), (200V, 100W) and (200V, 25W) respectively. Find the current through each bulb and which bulb will give more light ?
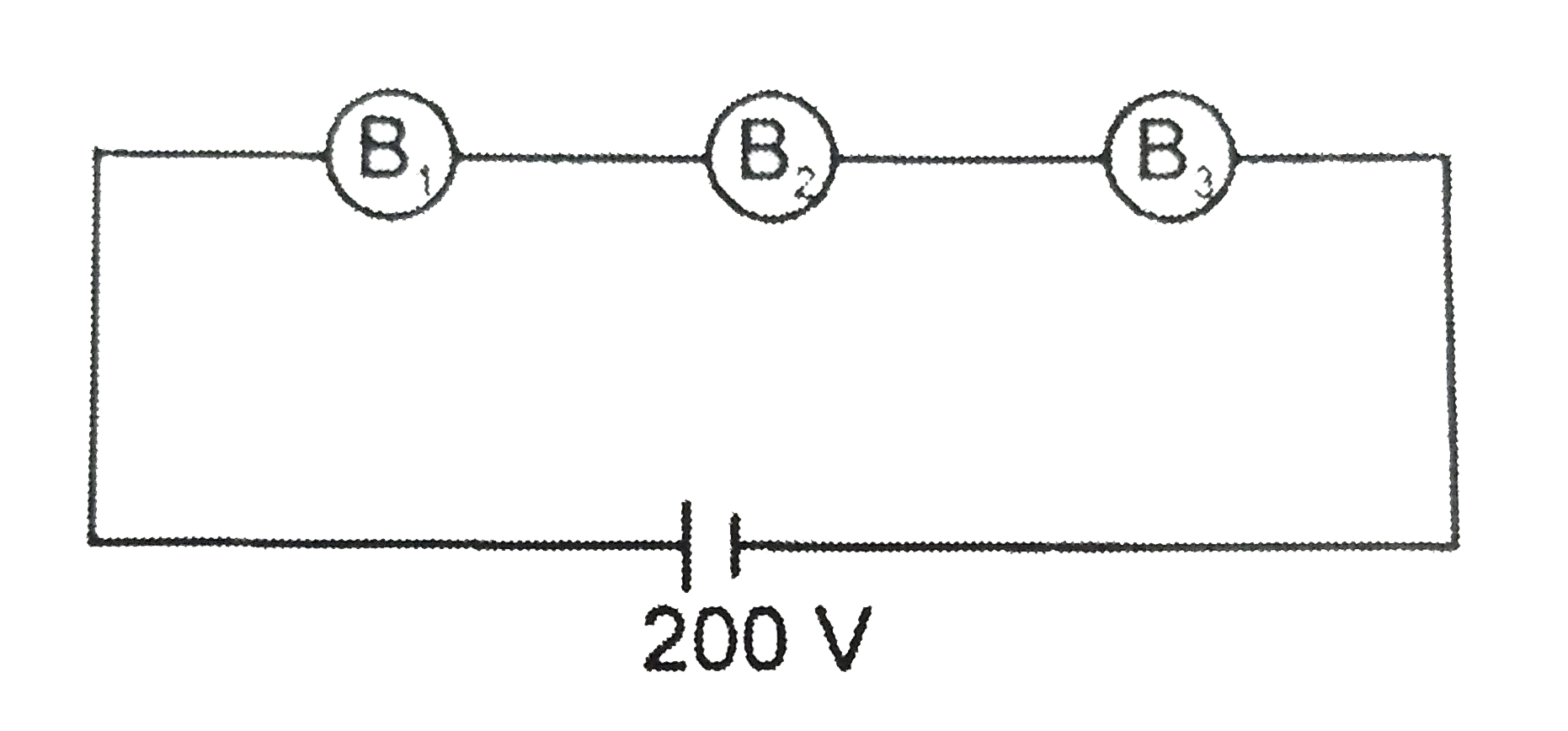 View Solution
View SolutionThe supply voltage to room is 120 V. The resistance of the lead wires is 6Ω. A 60 W bulb is already switched on. What is the decrease of voltage across the bulb, when a 240 W heater is switched on in parallel to the bulb?
View SolutionThe specification on a heater coil is 250V,500W. Calculate the resistance of the coil. What will be the resistance of a coil of 1000W to operate at the same voltage?
View SolutionTwo electric bulbs , rated for the same voltage , have powers of 200Wand100W, respectively. If their resistances are r1andr2 , respectively , then
View SolutionThe temperature coefficient of resistance for two material A and B are 0.0031∘C−1 and 0.0068∘C−1 respectively .Two resistance R1andR2 made from material A and B respectively . Have resistance of 200Ω and 100Ω at 0∘C. Show as a diagram the colour cube of a carbon resistance that would have a resistance equal to the series combination of R1andR2 at a temperature of 100∘C (Neglect the ring corresponding to the tolerance of the carbon resistor)
View SolutionThree resistors R1,R2 and R3 are to be combined to form an electrical circuit as shown in the figure. It is found that when R1R2andR3 are put respectively in positions A, B and C, the effective resistance of the circuit is 70 ΩWhen R2,R3andR1 are put respectively in position A, B and C the effective resistance is 35Ω and when R3,R1andR2 are respectively put in the position A, B and C, the effective resistance is 42Ω
If R1,R2 andR3are put in series, the effective resistance will beView Solution
