Using Ampere.s circuital law, obtain an expression for the magnetic flux density .B. at a point .X. at a perpendicular distance .r. from a long current carrying conductor. (Statement of the law is not required).
The figure shows a circular loop of radius r around an infinitely long straight wire carrying current I.
As the field lines are circular, the field →B at any point of the circular loop is directed along the tangent to the circle at that point. By symmetry, the magnitude of field →B is same at every point of the circular loop.
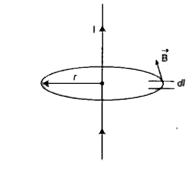
Therefore, ∮→B.→dl=∮Bdlcos0∘=B∮dl=B.2πr
From Ampere.s circuital law,
∮→B.→dl=μ0I
⇒B.2πr=u0I
∴B=μ0I2πr
Similar Questions
(a) Using Ampere.s circuital law or Biot Savart.s law, show that magnetic flux density .B. at a point P at a perpendicular distance.d from a long current carrying conductor is given by: B=(μ04π)2Ia (Statement of the law is not required)
(b) Define the terms (i) drift velocity, (ii) relaxation time. A conductor of length L is connected to a d.c. source of emf E. If this conductor is replaced by another conductor of same material and same area of cross-section but of length 3L, how will the drift velocity change?View SolutionUsing Ampere 's circuital law or Biot- Savart's a law, show that magnetic flux density B at point P at a perpendicular distance a from a long current carrying conductor is given by B=(μ4π)2Ia [ Statement of the laws not required]
View SolutionUsing Ampere.s Circuital Law, derive an expression for the magnetic field along the axis of a toroidal solenoid.
View SolutionThe magnetic flux density at a point distant d from a long straight current carrying conductor is B, then its value at distance d2 will be-
View SolutionObtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I.
View SolutionObtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I.
View SolutionUsing Ampere's circuital law, obtain an expression for the magnetic field along the axis of a current carrying solenoid of length l and having N number of turns.
View Solution(a)Using Ampere's circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis.
(b )How is the magnetic field inside a given solenoid made strong?View SolutionWhich of the following figure shown the magnetic flux denstiy b at a distance r from a long straight rod carrying a steady current I ?
View SolutionFind magnetic flux density at a point on the axis of a long solenoid having 5000 turns/m when it carrying a current of 2 A
View Solution

