An infinite line charge Produces a field of 9x104NC−1 at a distance of 3 cm. Calculate the linear charge density.
To solve the problem of calculating the linear charge density (λ) produced by an infinite line charge that generates an electric field (E) of 9×104N/C at a distance of 3 cm, we can follow these steps:
Step 1: Understand the relationship between electric field and linear charge density
The electric field (E) produced by an infinite line charge is given by the formula:
E=14πϵ0⋅2λr
where:
- E is the electric field,
- λ is the linear charge density,
- r is the distance from the line charge,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
Step 2: Rearrange the formula to solve for λ
To find the linear charge density λ, we can rearrange the formula:
λ=E⋅r⋅4πϵ02
Step 3: Convert the distance from centimeters to meters
The distance given is 3 cm. We need to convert this to meters:
r=3cm=3×10−2m
Step 4: Substitute the known values into the equation
Now we can substitute the values into the rearranged formula. We know:
- E=9×104N/C
- r=3×10−2m
- ϵ0=8.85×10−12C2/N m2
Substituting these values:
λ=(9×104)⋅(3×10−2)⋅(4π⋅8.85×10−12)2
Step 5: Calculate the value of λ
First, calculate 4πϵ0:
4πϵ0≈4⋅3.14⋅8.85×10−12≈1.112×10−10C2/N m2
Now substitute this back into the equation for λ:
λ=(9×104)⋅(3×10−2)⋅(1.112×10−10)2
Calculating this step-by-step:
1. Calculate 9×104×3×10−2=2.7×103
2. Now multiply by 1.112×10−10:
2.7×103×1.112×10−10≈3.006×10−7
3. Finally, divide by 2:
λ≈3.006×10−72≈1.503×10−7C/m
Final Answer
The linear charge density λ is approximately:
λ≈1.503×10−7C/m
The electric field (E) produced by an infinite line charge is given by the formula:
E=14πϵ0⋅2λr
where:
- E is the electric field,
- λ is the linear charge density,
- r is the distance from the line charge,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
To find the linear charge density λ, we can rearrange the formula:
λ=E⋅r⋅4πϵ02
The distance given is 3 cm. We need to convert this to meters:
r=3cm=3×10−2m
Now we can substitute the values into the rearranged formula. We know:
- E=9×104N/C
- r=3×10−2m
- ϵ0=8.85×10−12C2/N m2
λ=(9×104)⋅(3×10−2)⋅(4π⋅8.85×10−12)2
First, calculate 4πϵ0:
4πϵ0≈4⋅3.14⋅8.85×10−12≈1.112×10−10C2/N m2
Now substitute this back into the equation for λ:
λ=(9×104)⋅(3×10−2)⋅(1.112×10−10)2
Calculating this step-by-step:
1. Calculate 9×104×3×10−2=2.7×103
2. Now multiply by 1.112×10−10:
2.7×103×1.112×10−10≈3.006×10−7
3. Finally, divide by 2:
λ≈3.006×10−72≈1.503×10−7C/m
The linear charge density λ is approximately:
λ≈1.503×10−7C/m
Similar Questions
An infinite line charge produces a field of 9×10−4NC−1 at a distance of 2 cm. Calculate the linear charge density.
View SolutionAn infinite line charge produces a field of 9×104NC at a distance of 2cm. Calculate the linear charge density.
View SolutionAn infinite line charge produces a field of 18×104 N/C at a distance of 2 metre from it. The linear charge density is
View SolutionAn infinite line charge produces a field of 7.182×108N/C at distance of 2 cm. the linear charge density is
View SolutionTwo infinite linear charges are placed parallel to each other at a distance 0.1m from each other. If the linear charge density on each is 5μC/m, then the force acting on a unit length of each linear charge will be:
View SolutionAn electric dipole consists of charges ±2.0×10−8 C separated by distance of ±2.0×10−3m. It is placed at a distance of 6 cm from a line charge of linear charge density 4.0×10−4Cm−1 as shown in figure such that the dipole makes an angle of θ=60∘ with line AB. Find the force acting on the dipole.

View SolutionAn electric dipole consists of charges ±2.0×10−8C separated by a distance of 2.0×10−3 m. It is placed near a long line charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such that the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.

View SolutionAn electric dipole consists of charges ±2.0×108C separated by a distance of 2.0×10−3 m. It is placed near a long ilne charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such thet the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.

View SolutionAn infinite number of charges, each equal to Q=10μC are placed along the x-axis at x=1,3,9…..m. Calculate the magnitude of electric field at x=0 if the consecutive charge have opposite signs.
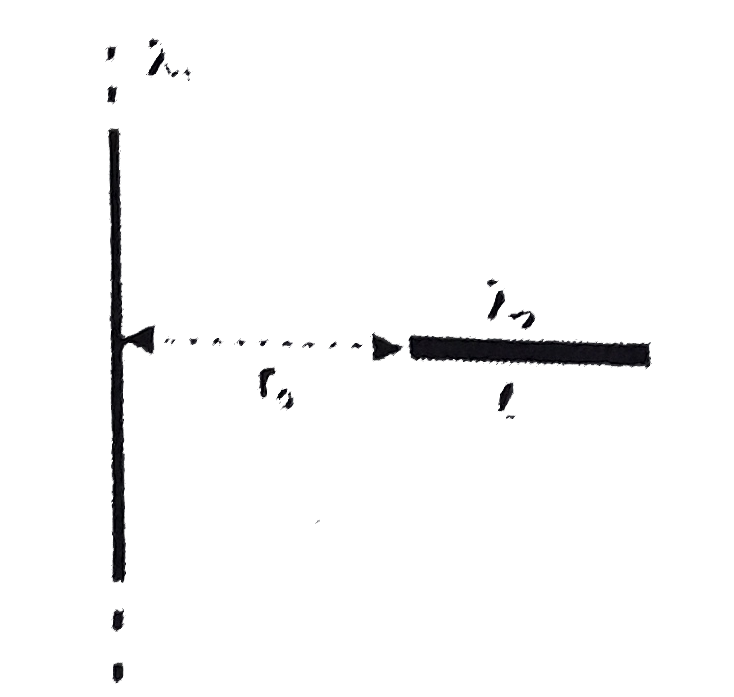
View SolutionAn infinitely long string uniformly charged with a linear charge density λ1 and a segment of length l uniformly charge with linear charge density λ2 lie in a plane at right angles to each other and separated by a distance r0 as shown in figure. The force with which these two interact is λ1λ24πε0ln(x). If l=r0, then find the value of x.
View Solution
