An infinite line charge produces a field of 9×10−4NC−1 at a distance of 2 cm. Calculate the linear charge density.
10μC/m
12μC/m
16μC/m
18μC/m
The correct Answer is:A
To solve the problem of finding the linear charge density (λ) of an infinite line charge that produces an electric field (E) of 9×10−4N/C at a distance (r) of 2 cm, we can follow these steps:
1. Identify the formula for the electric field due to an infinite line charge:
The electric field (E) produced by an infinite line charge is given by the formula:
E=14πϵ0⋅2λr
where:
- E is the electric field,
- λ is the linear charge density,
- r is the distance from the line charge,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/(N⋅m2).
2. Rearrange the formula to solve for linear charge density (λ):
We can rearrange the formula to isolate λ:
λ=E⋅r⋅4πϵ02
3. Convert the distance from centimeters to meters:
The distance given is 2 cm. We need to convert this to meters:
r=2cm=0.02m
4. Substitute the known values into the equation:
Now we can substitute the known values into the rearranged formula:
- E=9×10−4N/C
- r=0.02m
- ϵ0≈8.85×10−12C2/(N⋅m2)
Plugging in these values:
λ=(9×10−4)⋅(0.02)⋅(4π⋅8.85×10−12)2
5. Calculate the value of λ:
First, calculate 4πϵ0:
4πϵ0≈4⋅3.14⋅8.85×10−12≈1.11×10−10C2/(N⋅m2)
Now substitute this back into the equation:
λ=(9×10−4)⋅(0.02)⋅(1.11×10−10)2
λ=(1.998×10−15)2≈9.99×10−16C/m
6. Final result:
The linear charge density (λ) is approximately:
λ≈1.0×10−7C/m
The electric field (E) produced by an infinite line charge is given by the formula:
E=14πϵ0⋅2λr
where:
- E is the electric field,
- λ is the linear charge density,
- r is the distance from the line charge,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/(N⋅m2).
We can rearrange the formula to isolate λ:
λ=E⋅r⋅4πϵ02
The distance given is 2 cm. We need to convert this to meters:
r=2cm=0.02m
Now we can substitute the known values into the rearranged formula:
- E=9×10−4N/C
- r=0.02m
- ϵ0≈8.85×10−12C2/(N⋅m2)
λ=(9×10−4)⋅(0.02)⋅(4π⋅8.85×10−12)2
First, calculate 4πϵ0:
4πϵ0≈4⋅3.14⋅8.85×10−12≈1.11×10−10C2/(N⋅m2)
Now substitute this back into the equation:
λ=(9×10−4)⋅(0.02)⋅(1.11×10−10)2
λ=(1.998×10−15)2≈9.99×10−16C/m
The linear charge density (λ) is approximately:
λ≈1.0×10−7C/m
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise
34 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERT ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - All Questions
32 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
17 Videos
Similar Questions
An infinite line charge Produces a field of 9x104NC−1 at a distance of 3 cm. Calculate the linear charge density.
View SolutionAn infinite line charge produces a field of 9×104NC at a distance of 2cm. Calculate the linear charge density.
View SolutionAn infinite line charge produces a field of 18×104 N/C at a distance of 2 metre from it. The linear charge density is
View SolutionAn infinite line charge produces a field of 7.182×108N/C at distance of 2 cm. the linear charge density is
View SolutionTwo infinite linear charges are placed parallel to each other at a distance 0.1m from each other. If the linear charge density on each is 5μC/m, then the force acting on a unit length of each linear charge will be:
View SolutionAn electric dipole consists of charges ±2.0×10−8 C separated by distance of ±2.0×10−3m. It is placed at a distance of 6 cm from a line charge of linear charge density 4.0×10−4Cm−1 as shown in figure such that the dipole makes an angle of θ=60∘ with line AB. Find the force acting on the dipole.

View SolutionAn electric dipole consists of charges ±2.0×10−8C separated by a distance of 2.0×10−3 m. It is placed near a long line charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such that the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.

View SolutionAn electric dipole consists of charges ±2.0×108C separated by a distance of 2.0×10−3 m. It is placed near a long ilne charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such thet the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.

View SolutionA Charged particle of mass 1.0 g is suspended through a
. silk thread of length 40 cm in a horizantal electric field
. of 4.0×104NC−1 . If the particle stays aty a distance of
. 24 cm from the wall in equilibrium, find the charge on
. the particle.
View SolutionAn infinitely long string uniformly charged with a linear charge density λ1 and a segment of length l uniformly charge with linear charge density λ2 lie in a plane at right angles to each other and separated by a distance r0 as shown in figure. The force with which these two interact is λ1λ24πε0ln(x). If l=r0, then find the value of x.
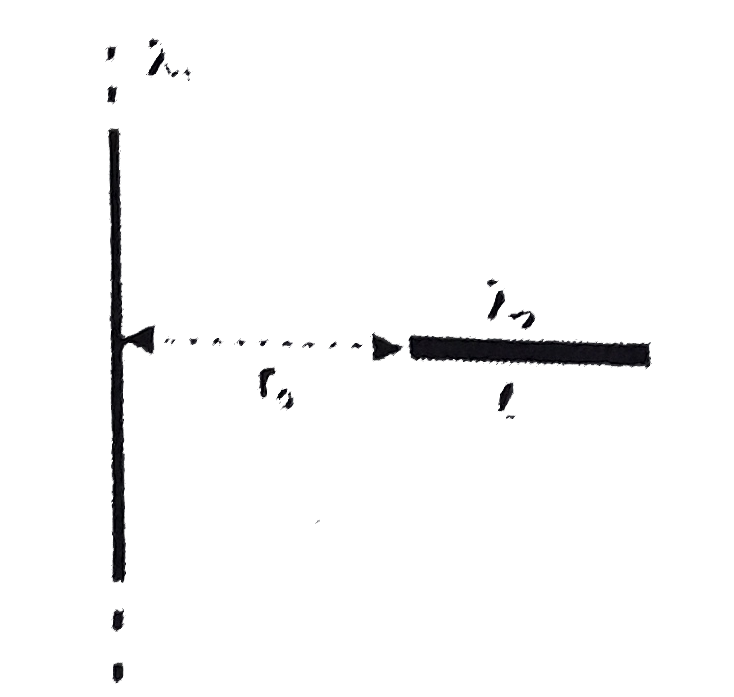
View Solution
