An infinite line charge produces a field of 9×104NC at a distance of 2cm. Calculate the linear charge density.
To solve the problem of calculating the linear charge density from the given electric field produced by an infinite line charge, we can follow these steps:
1. Understand the Formula: The electric field E due to an infinite line charge is given by the formula:
E=λ2πϵ0r
where:
- E is the electric field intensity,
- λ is the linear charge density,
- ϵ0 is the permittivity of free space (8.85×10−12C2/N m2),
- r is the distance from the line charge.
2. Identify Given Values: From the problem statement, we have:
- E=9×104N/C
- r=2cm=2×10−2m
3. Rearrange the Formula: We need to rearrange the formula to solve for λ:
λ=E⋅2πϵ0r
4. Substitute the Values: Now, substitute the known values into the rearranged formula:
λ=(9×104)⋅(2π⋅8.85×10−12)⋅(2×10−2)
5. Calculate 2πϵ0: First, calculate 2πϵ0:
2π⋅8.85×10−12≈5.57×10−11C2/N m2
6. Multiply the Values: Now, substitute this back into the equation for λ:
λ=(9×104)⋅(5.57×10−11)⋅(2×10−2)
7. Perform the Multiplication:
- First, calculate 9×2=18
- Then, calculate 18×5.57≈100.26
- Finally, multiply by 104⋅10−11⋅10−2=10−9
Thus,
λ≈100.26×10−9C/m=1.0026×10−7C/m
8. Convert to Microcoulombs: To express this in microcoulombs per meter:
λ≈10.03μC/m
Final Answer:
The linear charge density λ is approximately 10μC/m.
E=λ2πϵ0r
where:
- E is the electric field intensity,
- λ is the linear charge density,
- ϵ0 is the permittivity of free space (8.85×10−12C2/N m2),
- r is the distance from the line charge.
- E=9×104N/C
- r=2cm=2×10−2m
λ=E⋅2πϵ0r
λ=(9×104)⋅(2π⋅8.85×10−12)⋅(2×10−2)
2π⋅8.85×10−12≈5.57×10−11C2/N m2
λ=(9×104)⋅(5.57×10−11)⋅(2×10−2)
- First, calculate 9×2=18
- Then, calculate 18×5.57≈100.26
- Finally, multiply by 104⋅10−11⋅10−2=10−9
λ≈100.26×10−9C/m=1.0026×10−7C/m
λ≈10.03μC/m
The linear charge density λ is approximately 10μC/m.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 5
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 6
4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
An infinite line charge produces a field of 9×10−4NC−1 at a distance of 2 cm. Calculate the linear charge density.
View SolutionAn infinite line charge Produces a field of 9x104NC−1 at a distance of 3 cm. Calculate the linear charge density.
View SolutionAn infinite line charge produces a field of 18×104 N/C at a distance of 2 metre from it. The linear charge density is
View SolutionAn infinite line charge produces a field of 7.182×108N/C at distance of 2 cm. the linear charge density is
View SolutionTwo infinite linear charges are placed parallel to each other at a distance 0.1m from each other. If the linear charge density on each is 5μC/m, then the force acting on a unit length of each linear charge will be:
View SolutionAn electric dipole consists of charges ±2.0×10−8 C separated by distance of ±2.0×10−3m. It is placed at a distance of 6 cm from a line charge of linear charge density 4.0×10−4Cm−1 as shown in figure such that the dipole makes an angle of θ=60∘ with line AB. Find the force acting on the dipole.

View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
_2019_CBT2_E01_009_Q01.png)
View SolutionA positive charge is released from rest at a distance r0 from a positive line charge with uniform density . The speed (v) of the point charge , as a function of instantaneous distance r from line charge, is proportional to:
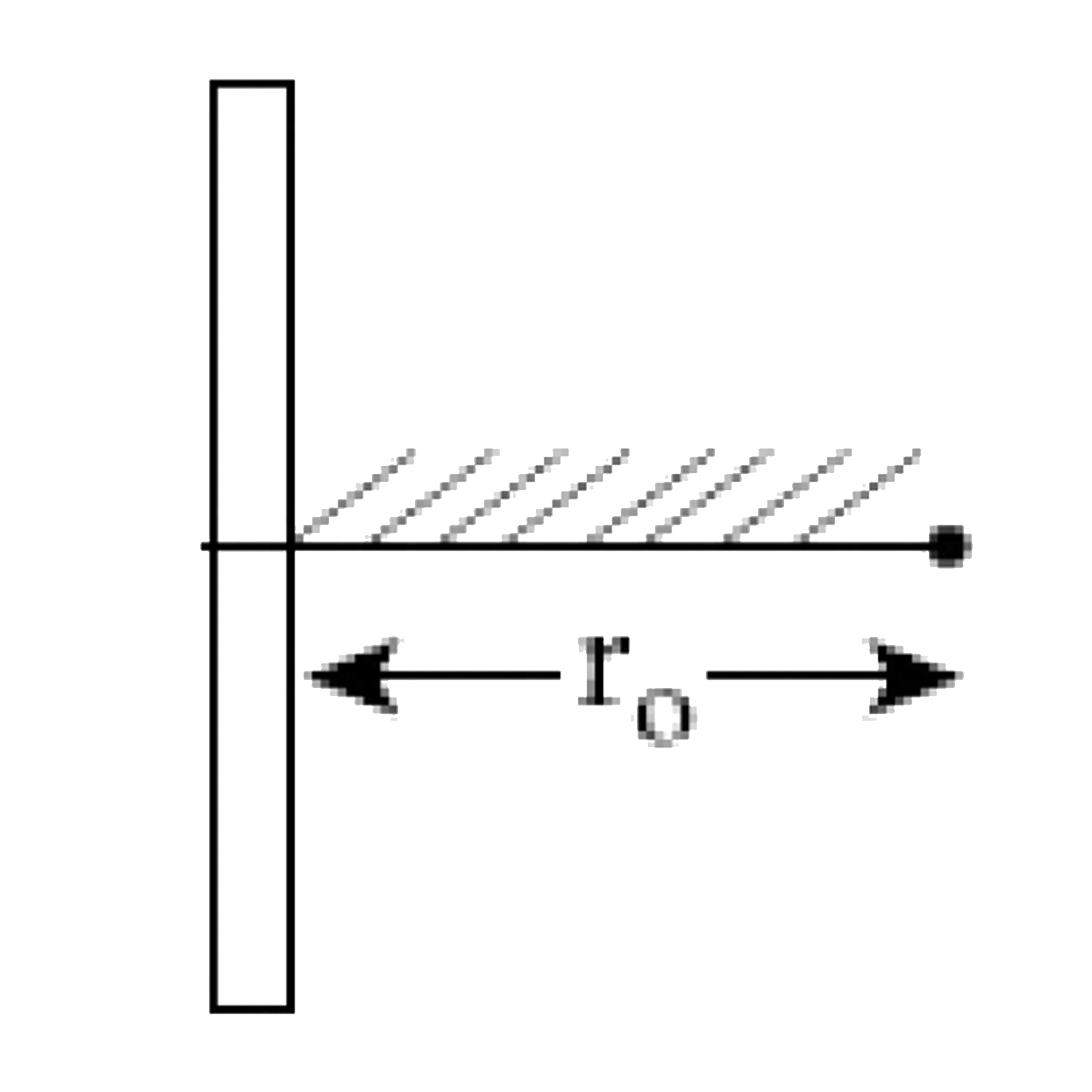
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionAn electric dipole consists of charges ±2.0×10−8C separated by a distance of 2.0×10−3 m. It is placed near a long line charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such that the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.

View Solution
