cells each of emf e and internal resistance r are joined in series to form a row and such rows are connected in parallel to form a battery of N = mn cells. If this battery is connected to an external resistance R.
Show that current f flowing through the external resistance R is given by :
I=NemR+nr
To solve the problem, we need to analyze the arrangement of the cells, their equivalent EMF, and the equivalent internal resistance when connected in series and parallel. Here’s a step-by-step breakdown:
Step 1: Understand the Configuration
We have cells, each with an EMF e and internal resistance r. There are n cells connected in series to form one row. Since there are m such rows connected in parallel, we can denote the total number of cells as N=mn.
Step 2: Calculate the EMF and Internal Resistance of One Row
When n cells are connected in series:
- The total EMF of the row is:
Erow=n⋅e
- The total internal resistance of the row is:
Rrow=n⋅r
Step 3: Calculate the Equivalent EMF and Internal Resistance of the Battery
Now, we have m rows connected in parallel. The equivalent EMF for the entire battery remains the same as that of one row:
Ebattery=n⋅e
The equivalent internal resistance of m rows in parallel is given by:
Rbattery=Rrowm=n⋅rm
Step 4: Connect to External Resistance
The battery is connected to an external resistance R. The total resistance in the circuit is the sum of the internal resistance of the battery and the external resistance:
Rtotal=R+Rbattery=R+n⋅rm
Step 5: Apply Ohm’s Law to Find the Current
Using Ohm's law, the current I flowing through the external resistance R can be calculated as:
I=EbatteryRtotal=n⋅eR+n⋅rm
Step 6: Simplify the Expression
To simplify the expression for current:
I=n⋅eR+n⋅rm=n⋅emR+n⋅rm=n⋅e⋅mmR+n⋅r
Since we can express N=mn, we can write:
I=N⋅emR+n⋅r
Final Result
Thus, the current I flowing through the external resistance R is given by:
I=N⋅emR+n⋅r
We have cells, each with an EMF e and internal resistance r. There are n cells connected in series to form one row. Since there are m such rows connected in parallel, we can denote the total number of cells as N=mn.
When n cells are connected in series:
- The total EMF of the row is:
Erow=n⋅e
- The total internal resistance of the row is:
Rrow=n⋅r
Now, we have m rows connected in parallel. The equivalent EMF for the entire battery remains the same as that of one row:
Ebattery=n⋅e
The equivalent internal resistance of m rows in parallel is given by:
Rbattery=Rrowm=n⋅rm
The battery is connected to an external resistance R. The total resistance in the circuit is the sum of the internal resistance of the battery and the external resistance:
Rtotal=R+Rbattery=R+n⋅rm
Using Ohm's law, the current I flowing through the external resistance R can be calculated as:
I=EbatteryRtotal=n⋅eR+n⋅rm
To simplify the expression for current:
I=n⋅eR+n⋅rm=n⋅emR+n⋅rm=n⋅e⋅mmR+n⋅r
Since we can express N=mn, we can write:
I=N⋅emR+n⋅r
Thus, the current I flowing through the external resistance R is given by:
I=N⋅emR+n⋅r
Similar Questions
cells each of emf e and internal resistance r are joined in series to form a row and such rows are connected in parallel to form a battery of N = mn cells. If this battery is connected to an external resistance R.
What is the emf of this battery and how much is its internal resistance ?
View Solutionn. cells, each of emf .e. and internal resistance .r. are joined in series to form a row. .m. such rows are connected in parallel to form a battery of N = mn cells. This battery is connected to an external resistance .R..
(i) What is the emf of this battery and how much is its internal resistance ?
Show that current .l. flowing through the external resistance .R. is given by-
I=NemR+nr
View Solution
Knowledge Check
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr
n identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
View SolutionN cells each of e.m.f. E & internal resistance r are grouped into sets of K cells connected in series. The (N/K) sets ae connected in parallel to a load of resistance R, then,
View SolutionConsider N=n1n2indentical cells, each of emf(ε) and internal resistance r. Suppose n1 cells are joined in series to forn a line and n_(2) such are connected in parallel. The combination drives a current in an external resistance R.(a) find the current in the external resistance, (b) Assuming that n1and n_(2) can be continuously varied, find the relation between n_(1) ,n_(2) R and r for which the current in R in maximum.
View SolutionA group of n identical cells each of EMF E and internal resistance r are joined in series to form a loop as shown . The terminal voltage across each cell is
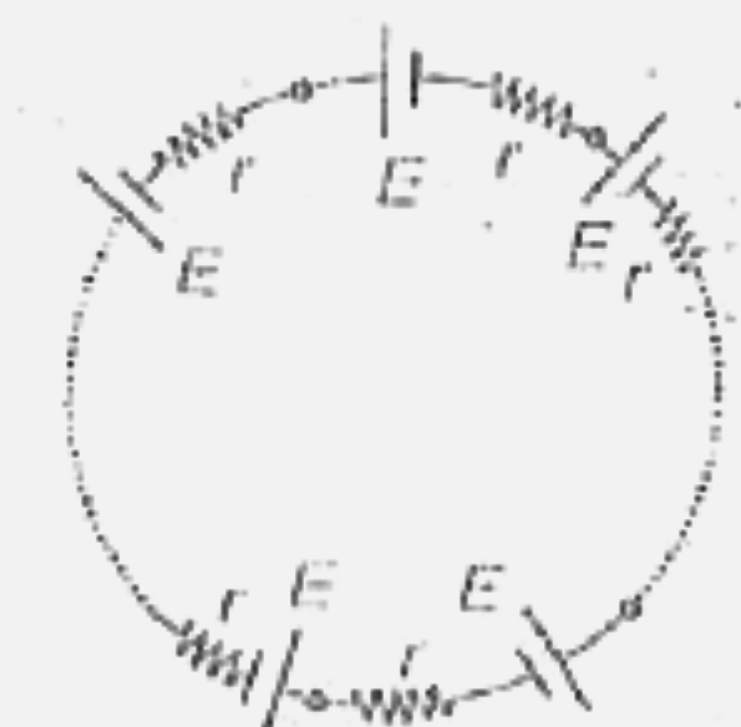
View SolutionA group of six identical cells each of emf E and internal resistance r are joined in series to form a loop. The terminal voltage across each cells is
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View Solution
