cells each of emf e and internal resistance r are joined in series to form a row and such rows are connected in parallel to form a battery of N = mn cells. If this battery is connected to an external resistance R.
What is the emf of this battery and how much is its internal resistance ?
To solve the problem, we need to determine the equivalent electromotive force (emf) and the internal resistance of a battery formed by cells connected in series and parallel. Let's break it down step by step.
Step 1: Understand the Configuration
We have N=mn cells, where:
- Each cell has an emf of e and an internal resistance of r.
- The cells are arranged in m rows, with each row containing n cells in series.
Step 2: Calculate the Equivalent Emf of One Row
When cells are connected in series, the total emf is the sum of the individual emfs. Therefore, for n cells in series, the equivalent emf of one row (let's call it Erow) is:
\(
E_{\text{row}} = n \cdot e
\)
Step 3: Calculate the Internal Resistance of One Row
The internal resistance of cells in series adds up. Thus, the equivalent internal resistance (let's call it rrow) for one row is:
\(
r_{\text{row}} = n \cdot r
\)
Step 4: Calculate the Equivalent Emf of the Battery
Now, we have m such rows connected in parallel. The emf of the entire battery remains the same as that of one row because in parallel, the voltage remains constant. Therefore, the equivalent emf of the battery (let's call it Ebaery) is:
\(
E_{\text{battery}} = E_{\text{row}} = n \cdot e
\)
Step 5: Calculate the Equivalent Internal Resistance of the Battery
For m rows connected in parallel, the equivalent internal resistance (let's call it rbaery) can be calculated using the formula for resistances in parallel:
\(
\frac{1}{r_{\text{battery}}} = \frac{1}{r_{\text{row}}} + \frac{1}{r_{\text{row}}} + \ldots + \frac{1}{r_{\text{row}}} \quad (m \text{ times})
\)
This simplifies to:
\(
\frac{1}{r_{\text{battery}}} = \frac{m}{r_{\text{row}}} = \frac{m}{n \cdot r}
\)
Taking the reciprocal gives:
\(
r_{\text{battery}} = \frac{n \cdot r}{m}
\)
Final Results
Thus, the equivalent emf of the battery is:
\(
E_{\text{battery}} = n \cdot e
\)
And the internal resistance of the battery is:
\(
r_{\text{battery}} = \frac{n \cdot r}{m}
\)
We have N=mn cells, where:
- Each cell has an emf of e and an internal resistance of r.
- The cells are arranged in m rows, with each row containing n cells in series.
When cells are connected in series, the total emf is the sum of the individual emfs. Therefore, for n cells in series, the equivalent emf of one row (let's call it Erow) is:
\(
E_{\text{row}} = n \cdot e
\)
The internal resistance of cells in series adds up. Thus, the equivalent internal resistance (let's call it rrow) for one row is:
\(
r_{\text{row}} = n \cdot r
\)
Now, we have m such rows connected in parallel. The emf of the entire battery remains the same as that of one row because in parallel, the voltage remains constant. Therefore, the equivalent emf of the battery (let's call it Ebaery) is:
\(
E_{\text{battery}} = E_{\text{row}} = n \cdot e
\)
For m rows connected in parallel, the equivalent internal resistance (let's call it rbaery) can be calculated using the formula for resistances in parallel:
\(
\frac{1}{r_{\text{battery}}} = \frac{1}{r_{\text{row}}} + \frac{1}{r_{\text{row}}} + \ldots + \frac{1}{r_{\text{row}}} \quad (m \text{ times})
\)
This simplifies to:
\(
\frac{1}{r_{\text{battery}}} = \frac{m}{r_{\text{row}}} = \frac{m}{n \cdot r}
\)
Taking the reciprocal gives:
\(
r_{\text{battery}} = \frac{n \cdot r}{m}
\)
Thus, the equivalent emf of the battery is:
\(
E_{\text{battery}} = n \cdot e
\)
And the internal resistance of the battery is:
\(
r_{\text{battery}} = \frac{n \cdot r}{m}
\)
Similar Questions
n. cells, each of emf .e. and internal resistance .r. are joined in series to form a row. .m. such rows are connected in parallel to form a battery of N = mn cells. This battery is connected to an external resistance .R..
(i) What is the emf of this battery and how much is its internal resistance ?
Show that current .l. flowing through the external resistance .R. is given by-
I=NemR+nr
View Solutioncells each of emf e and internal resistance r are joined in series to form a row and such rows are connected in parallel to form a battery of N = mn cells. If this battery is connected to an external resistance R.
Show that current f flowing through the external resistance R is given by :
I=NemR+nr
View Solution
Knowledge Check
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr
n identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
View SolutionN identical cells, each of emf ε and internal resistances r are joined in series. Out of these, n cells are wrongly connected, i.e. their terminals are connected in reverse order as required for series connection. If εo be the emf of the resulting battery and ro be its internal resistance then for n <N/2
View SolutionN cells each of e.m.f. E & internal resistance r are grouped into sets of K cells connected in series. The (N/K) sets ae connected in parallel to a load of resistance R, then,
View SolutionA group of n identical cells each of EMF E and internal resistance r are joined in series to form a loop as shown . The terminal voltage across each cell is
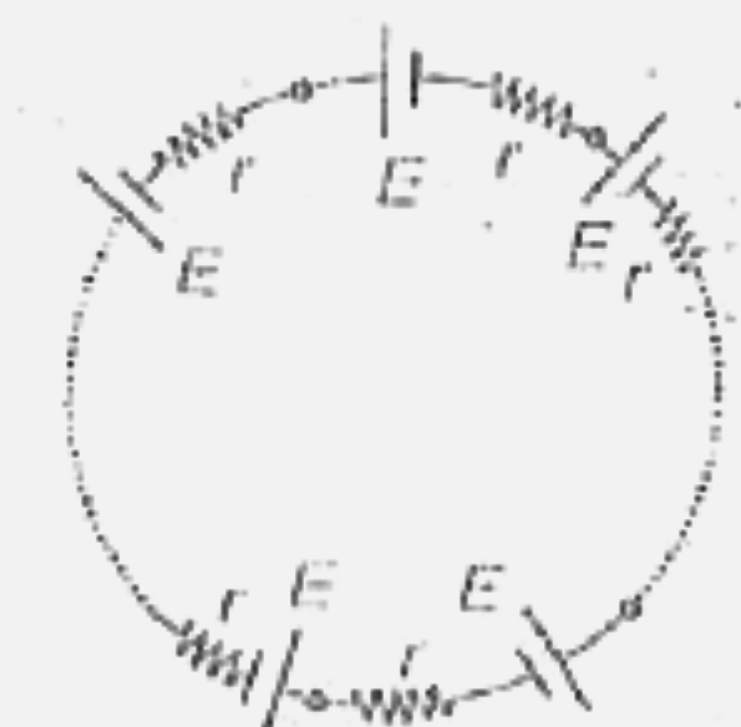
View SolutionA group of six identical cells each of emf E and internal resistance r are joined in series to form a loop. The terminal voltage across each cells is
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View Solution
