A square loop of 5 cm carrying a current 0.2 A in the clockwise direction is placed at a distance of 10 cm from an infinity long wire carrying a current of 1 A as shown. Calculate (i) the resultant magnetic force and (ii) the torque, if any, acting on the loop.
To solve the problem step by step, we will calculate the resultant magnetic force acting on the square loop and the torque, if any, acting on it.
Given Data:
- Length of the square loop (L) = 5 cm = 0.05 m
- Current in the loop (I_loop) = 0.2 A (clockwise)
- Current in the long wire (I_wire) = 1 A
- Distance from the wire to the loop (d) = 10 cm = 0.1 m
Step 1: Calculate the magnetic field (B) due to the long wire at the position of the loop.
The magnetic field (B) created by an infinite straight wire at a distance (r) is given by the formula:
B=μ0I2πr
Where:
- μ0=4π×10−7T m/A (permeability of free space)
- I=1A (current in the wire)
- r=0.1m (distance from the wire to the loop)
Substituting the values:
B=4π×10−7×12π×0.1=4×10−70.2=2×10−6T
Step 2: Calculate the magnetic force (F) on the loop.
The magnetic force (F) on a current-carrying conductor in a magnetic field is given by:
F=ILBsin(θ)
Where:
- I=0.2A (current in the loop)
- L=0.05m (length of one side of the loop)
- B=2×10−6T (magnetic field)
- θ=90∘ (angle between the current direction and magnetic field direction, since the loop is perpendicular to the field)
Substituting the values:
F=0.2×0.05×2×10−6×sin(90∘)=0.2×0.05×2×10−6=2×10−8N
Step 3: Determine the direction of the force.
The forces on opposite sides of the loop will be in opposite directions due to the direction of the current. The forces on the sides of the loop will be:
- Side AB (towards the wire): Attractive force (F_AB)
- Side CD (away from the wire): Repulsive force (F_CD)
Step 4: Calculate the net force acting on the loop.
The net force acting on the loop can be calculated by considering the forces on the sides of the loop:
Fnet=FAB−FCD
Since the forces are equal in magnitude but opposite in direction:
Fnet=2×10−8−2×10−8=0N
Step 5: Calculate the torque (τ) acting on the loop.
The torque (τ) on a current loop in a magnetic field is given by:
τ=nIABsin(θ)
Where:
- n=1 (number of turns in the loop)
- A=L2=(0.05)2=0.0025m2 (area of the loop)
- θ=90∘ (angle between the normal to the loop and the magnetic field)
Since the forces on opposite sides are equal and collinear, they do not produce any torque:
τ=0
Final Results:
1. The resultant magnetic force acting on the loop is Fnet=0N.
2. The torque acting on the loop is τ=0N m.
- Length of the square loop (L) = 5 cm = 0.05 m
- Current in the loop (I_loop) = 0.2 A (clockwise)
- Current in the long wire (I_wire) = 1 A
- Distance from the wire to the loop (d) = 10 cm = 0.1 m
The magnetic field (B) created by an infinite straight wire at a distance (r) is given by the formula:
B=μ0I2πr
Where:
- μ0=4π×10−7T m/A (permeability of free space)
- I=1A (current in the wire)
- r=0.1m (distance from the wire to the loop)
B=4π×10−7×12π×0.1=4×10−70.2=2×10−6T
The magnetic force (F) on a current-carrying conductor in a magnetic field is given by:
F=ILBsin(θ)
Where:
- I=0.2A (current in the loop)
- L=0.05m (length of one side of the loop)
- B=2×10−6T (magnetic field)
- θ=90∘ (angle between the current direction and magnetic field direction, since the loop is perpendicular to the field)
F=0.2×0.05×2×10−6×sin(90∘)=0.2×0.05×2×10−6=2×10−8N
The forces on opposite sides of the loop will be in opposite directions due to the direction of the current. The forces on the sides of the loop will be:
- Side AB (towards the wire): Attractive force (F_AB)
- Side CD (away from the wire): Repulsive force (F_CD)
The net force acting on the loop can be calculated by considering the forces on the sides of the loop:
Fnet=FAB−FCD
Since the forces are equal in magnitude but opposite in direction:
Fnet=2×10−8−2×10−8=0N
The torque (τ) on a current loop in a magnetic field is given by:
τ=nIABsin(θ)
Where:
- n=1 (number of turns in the loop)
- A=L2=(0.05)2=0.0025m2 (area of the loop)
- θ=90∘ (angle between the normal to the loop and the magnetic field)
τ=0
1. The resultant magnetic force acting on the loop is Fnet=0N.
2. The torque acting on the loop is τ=0N m.
Similar Questions
Answer the following:
(a) Define mutual inductance and write its S.I. unit.
(b) A square loop of side a carrying a current I2 is kept at distance x from an infinitely long straight wire carrying a current I1 as shown in the figure. Obtain the expression for the resultant force on the loop.

View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA square conducting loop is placed in the neighbourhood of a coplaner long straight wire carrying a current i.
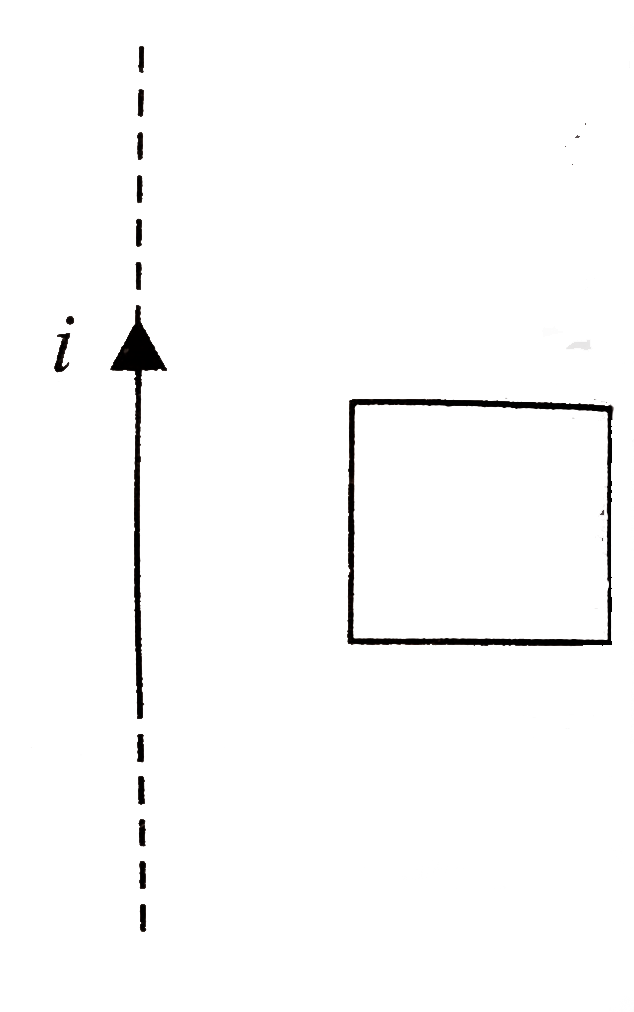
View SolutionTwo long parallel wires placed 0.08 m apart, carry currents 3 A and 5 A in the same direction. what is the distance from the conductor carrying the larger current to the point where the resultant magnetic field is zero?
View SolutionA square loop of side a is placed at a distance a length away from a long wire carrying a current I1 . If the loop carries a current I2 as shown in the figure . Then the nature of the nature of the force and its amount is

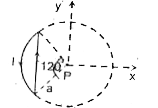
View SolutionA wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.

View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.

View SolutionA square loop PQRS carrying a current of 6.0 A is placed near a long wire carrying 10 A as shown in figure . (a) Show that the magnetic force acting on the part PQ is equal and opposite to that on the part RS. (b) Find the magnetic force on the square loop.

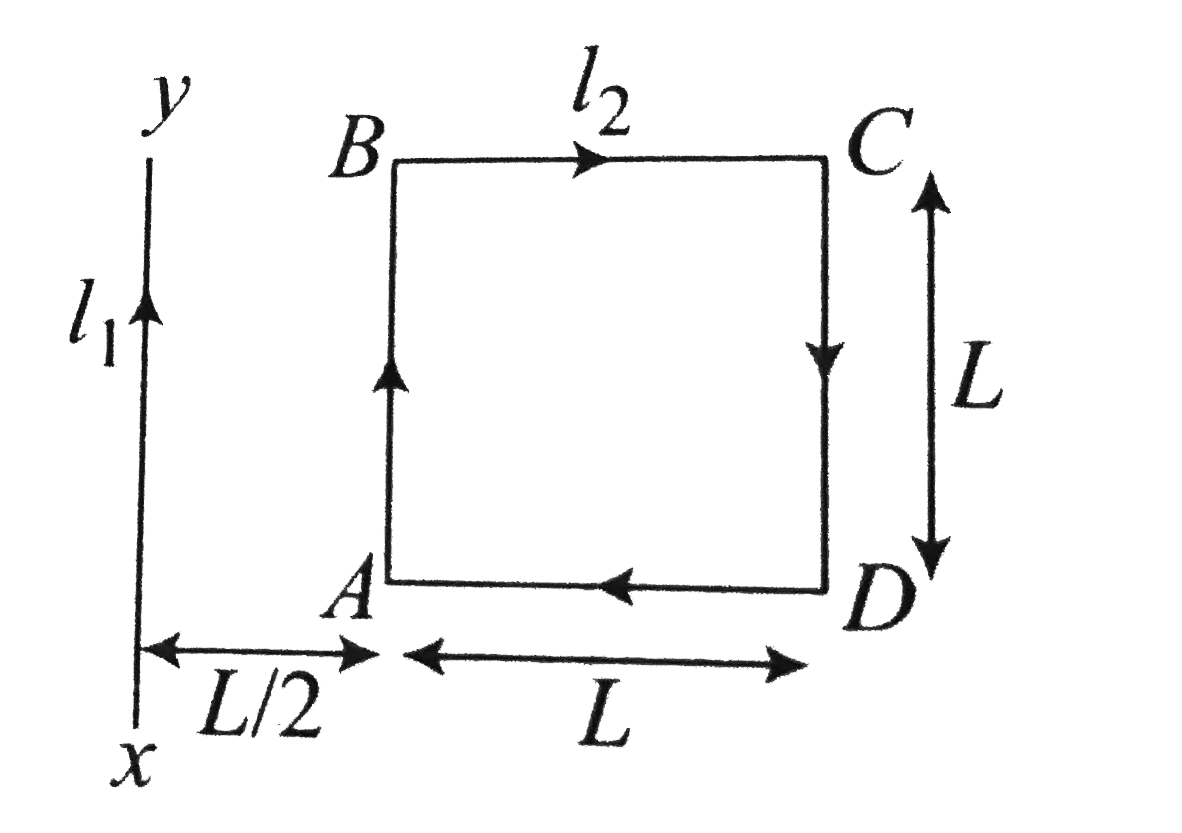
View SolutionA square loop ABCD, carrying a current I2 is placed near and coplanar with a long straight conductor XY, carrying a current I1 as shwon in Figure. The net force on the loop will be
View Solution
