A half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below.
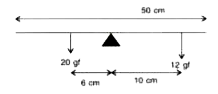
Which of the two forces acting on the rigid rod causes clockwise moment?
The force of 12 gf causes a clockwise moment.
Topper's Solved these Questions
Similar Questions
A half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below:
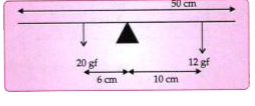
Is the rod in equilibrium ?View SolutionA half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below:
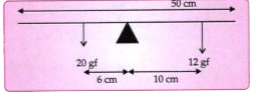
The direction of 20 kgf force is reversed. What is the magnitude of the resultant moment of the forces on the rod ?View Solution
Knowledge Check
- Question 1 - Select One
Find the weight of a metre scale balanced at 30cm mark such that two weights one of 30gf and 10gf are suspended at 5cm mark and 40cm mark respectively.
A10gfB105gfC25gfD32.5gf - Question 2 - Select One
Find the resultant moment of couple if two equal forces each of 6N are acting at a distance of 3cm each from the centre.
A36NmB360NmC3.6NmD0.36Nm
Two protons are a distance of 1×10−10cm from each other. The force acting on them are
View SolutionA rod is pivoted about its centre. A 10 N force is applied 4 m from the pivot and another force of 5 N is applied 2 m from the pivot, as shown. The magnitude of the total torque about the pivot is
 View Solution
View SolutionA body is pivoted at a point. A force of 10N is applied at a distance of 30cm from the pivot. Calculate the moment of force about the pivot.
View SolutionA very light rod of length l pivoted at O is connected with two springs of stiffness k1 & k2 at a distance of a & l from the pivot respectively. A block of mass ma attached with the spring k2 is kept on a smooth horizontal surface. Find the angular frequency of small oscillation of the block m.
_S01_031_Q01.png) View Solution
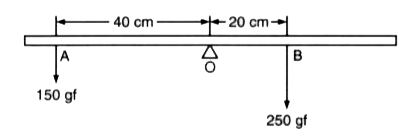
View SolutionThe diagram in Fig.1.34 shows a uniform metre rule weighing 100gf, pivoted at its centre O. Two weights 150 gf and 250 gf hang from the points A and B respectively of the metre rule such that OA= 40cm and OB=20cm . Calculate (i) the total anticlockwise moment about O, (ii) the total clockwise moment about O, (iii) the difference of anticlockwise and clockwise moments, and (iv) the distance from O where a 100gf weight should be placed to balanced the metre rule.
 View Solution
View SolutionA uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
Draw a diagram of the arrangement.View Solution

