Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.Solution in Assamese
Step by step video & image solution for Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The decimal expansion of 178 will terminate after how many places of decimals:
View SolutionForm the pair of linear equations in the following problems,and find their solution graphically.(i)10 students of class X took part in a Mathematics quiz.If the number of girls is 4 more than the number of boys,find the number of boys and girls who took part in the quiz.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
View SolutionThe ratio of area of Two similar triangles is equal to the ratio of the squares of any two corresponding sides.
View SolutionThe ratio of the the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides/altitudes.
View SolutionTheorem 6.6 : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
View SolutionThe ratio of areas of two similar triangles is equal to the ratio of the squares of corresponding…….
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that " the ratio of areas of two similar triangles is equal to the square of the ratio of their altitudes.
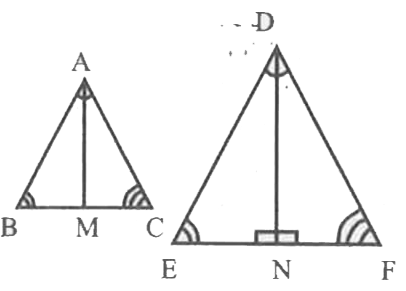
View Solutionprove that The areas of the two similar triangles are in the ratio of the square of the corresponding medians.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionTheorem 6.6 : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding altitudes of the triangles.
View Solution
