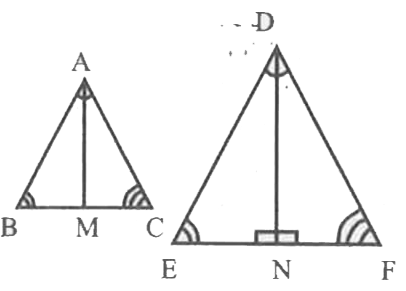
Prove that the ratio of altitudes of two similar triangles is equal to the ratio of their corresponding sides.Solution in Assamese
Step by step video & image solution for Prove that the ratio of altitudes of two similar triangles is equal to the ratio of their corresponding sides. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The ratio of the edges of a cuboid is 1:2:3 and its volume is 1,296cm3. What is the area of the whole surface?
View SolutionA line segment drawn parallel to the base BC of ΔABC intersects AB and AC at X and Y respectively.
If AB=7.2 , AC=4.8 and AX=4.2 then show that AY=2.8.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
View SolutionIf two triangles are similar; prove that the ratio of the corresponding sides is same as the ratio of corresponding medians.
View SolutionIf two triangles are similar; prove that the ratio of corresponding sides is equal to the ratio of corresponding altitudes.
View SolutionThe ratio of area of Two similar triangles is equal to the ratio of the squares of any two corresponding sides.
View SolutionProve that the area of two similar triangles are in ratio of the squares of the corresponding altitudes.
View SolutionThe corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
View SolutionThe ratio of the the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides/altitudes.
View SolutionProve that the ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding sides.
View SolutionThe perimeter of two similar triangles are in 4:9 ratio, the ratio of their corresponding sides is…………..
View SolutionThe ratio of the areas of two similar triangles is 1:4 then the ratio of their corresponding sides………….
View SolutionProve that " the ratio of areas of two similar triangles is equal to the square of the ratio of their altitudes.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that in two similar triangles the ratio of corresponding sides is equal to the ratio of the corresponding altitudes.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding altitudes of the triangles.
View Solution
