ABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
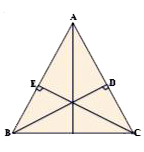 Solution in Telugu
Solution in Telugu
Step by step video & image solution for ABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that (i) DeltaABD ~= DeltaACE (ii) AB = AC i.e., ABC is an isosceles triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Can you give any two axioms from your daily life.
View SolutionIn the adjoining figure, BD = CE and ∠ADB=∠AEC=90∘, prove that
(i) ΔABD≅ΔACE (ii) ABC is an isosceles triangle.

View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionIn the following figure (not to scale), ABC is a right isosceles triangle, right- angle at B and BD⊥AC. If the triangle ABC is rotated about the hypotenuse, then find the locus of the triangle ABC. ltbr gt ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E02_006_Q01.png" width="80%"gt
View SolutionIn the figure (not to scale) AB = AC and BD = CD. Find ∠ADB
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E05_003_Q01.png" width="80%"gt
View SolutionABC is a triangle in which altitude BE and CF to sides AC and AB are equal. Show that
ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.

View SolutionABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively (see figure) Show that these altitudes are equal.
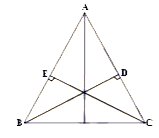
View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.

View SolutionABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively (see figure) Show that these altitudes are equal.
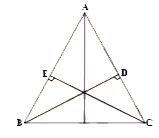
View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
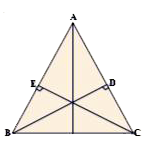
View SolutionABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively (see figure) Show that these altitudes are equal.
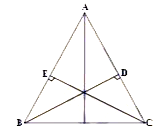
View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
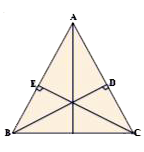
View SolutionABC एक त्रिभुज है जिसमे AC और AB पर खिचे गए शीर्षलम्ब BE और CF बराबर है ( देखिए आक्रति ) | दर्शाइए कि- (i) ΔABE ~-= ΔACF
(ii) AB -= AC, अर्थात ΔABC एक समद्धिबाहू त्रिभुज है |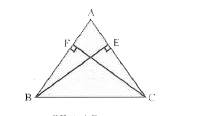
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that ( i ) △ABE≅△ACF
(ii) AB = AC i.e ABC is an isoceles triangle
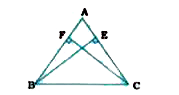
View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively (See Fig.
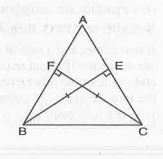 ). Show that these altitudes are equal.
). Show that these altitudes are equal.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (See Fig.
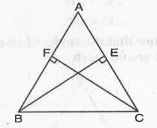 ). Show that AB = AC or ΔABC is an isosceles triangle.
). Show that AB = AC or ΔABC is an isosceles triangle.
View Solution
