A cylinderical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:

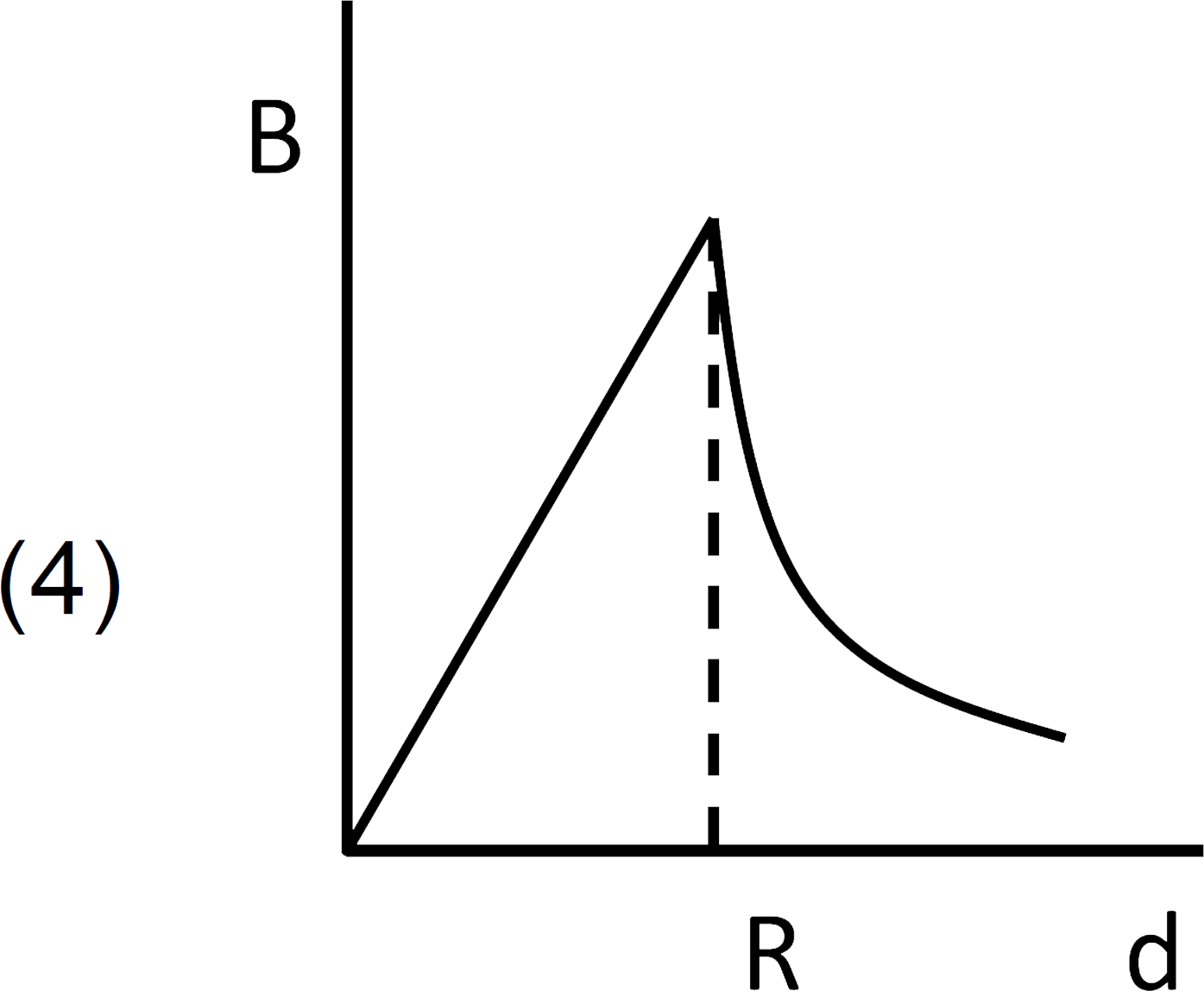
The correct Answer is:D
To solve the problem of determining the correct plot of the magnetic field B with respect to the distance d from the center of a cylindrical conductor carrying a constant current, we will follow these steps:
Step 1: Understand the Setup
We have a cylindrical conductor of radius R carrying a constant current I. We need to analyze the magnetic field inside and outside the conductor.
Step 2: Magnetic Field Inside the Conductor
For a point inside the cylindrical conductor at a distance d (where d<R), we can use Ampere's Circuital Law:
∮B⋅dl=μ0Ienc
The current density J can be defined as:
J=IA=IπR2
The enclosed current Ienc for a circular Amperian loop of radius d is:
Ienc=J⋅Aenc=J⋅πd2=IπR2⋅πd2=Id2R2
Using Ampere's law, we have:
B⋅2πd=μ0⋅Id2R2
Solving for B:
B=μ0Id2πR2
This shows that the magnetic field B inside the conductor is directly proportional to the distance d from the center.
Step 3: Magnetic Field Outside the Conductor
For a point outside the conductor at a distance d (where d>R), the entire current I is enclosed by the Amperian loop:
∮B⋅dl=μ0I
Thus, we have:
B⋅2πd=μ0I
Solving for B:
B=μ0I2πd
This shows that the magnetic field B outside the conductor is inversely proportional to the distance d from the center.
Step 4: Plotting the Magnetic Field
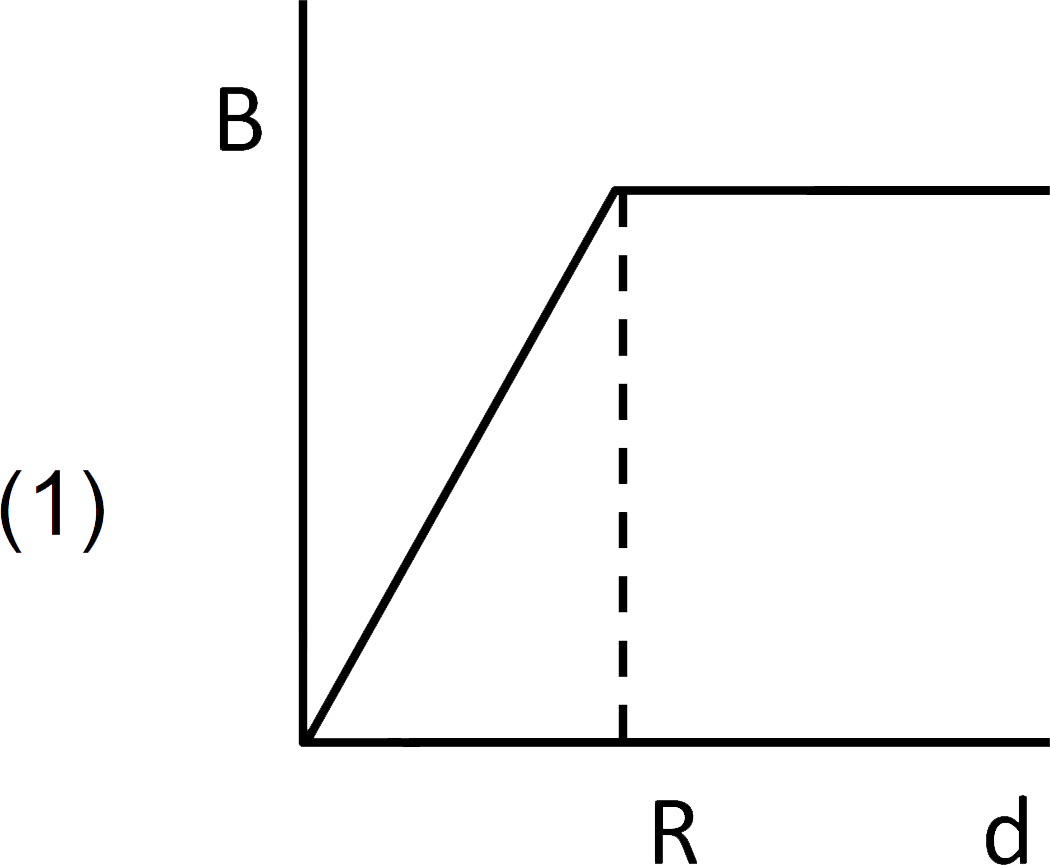
1. Inside the Conductor: The magnetic field increases linearly with d until d=R.
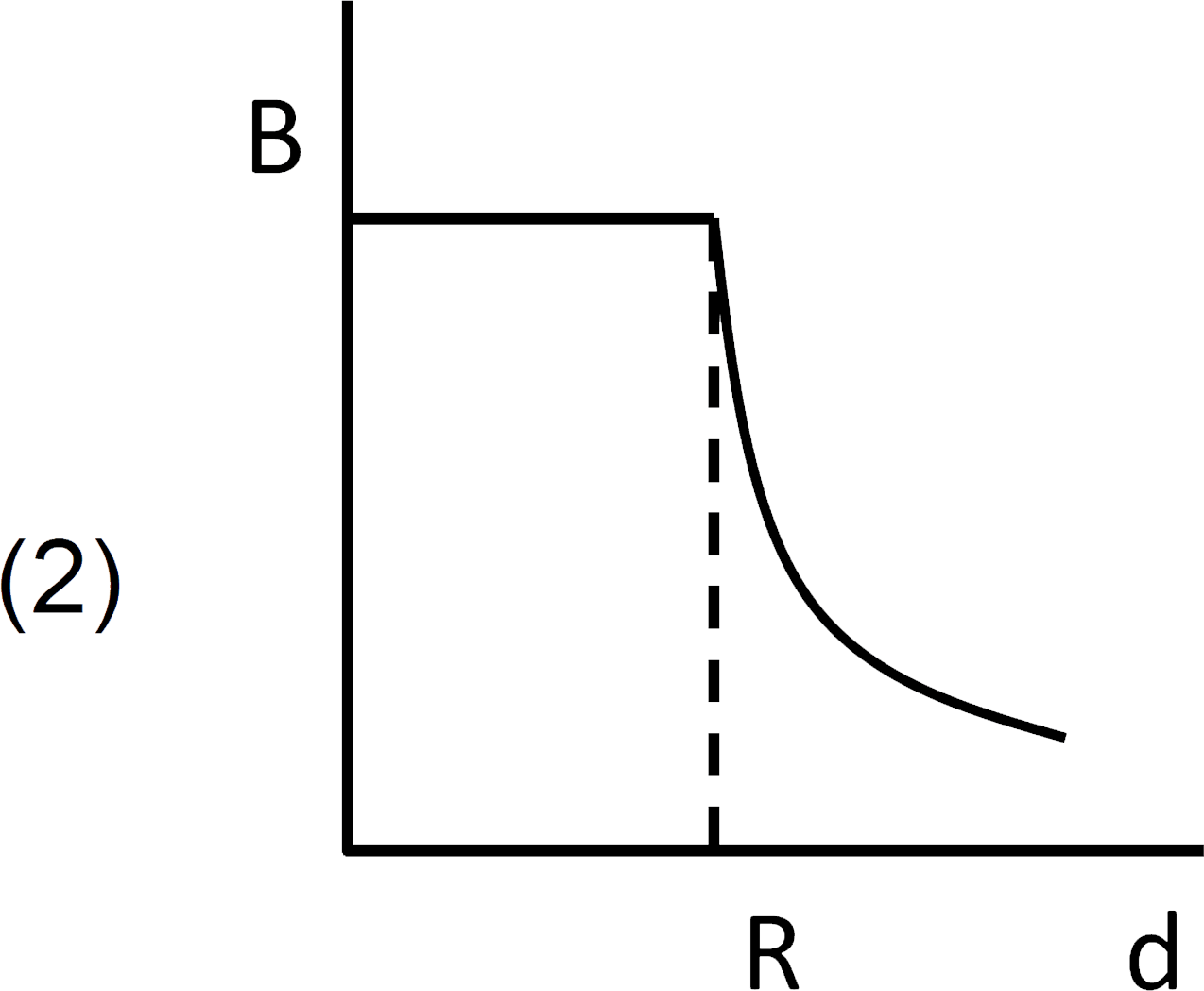
2. Outside the Conductor: The magnetic field decreases inversely with d after d=R.
Step 5: Conclusion
The correct representation of the magnetic field B as a function of distance d from the center of the cylindrical conductor is a graph that shows:
- A linear increase from the origin to d=R.
- A hyperbolic decrease for d>R.
Thus, the correct option that represents this behavior is Option 4.
---
We have a cylindrical conductor of radius R carrying a constant current I. We need to analyze the magnetic field inside and outside the conductor.
For a point inside the cylindrical conductor at a distance d (where d<R), we can use Ampere's Circuital Law:
For a point outside the conductor at a distance d (where d>R), the entire current I is enclosed by the Amperian loop:
1. Inside the Conductor: The magnetic field increases linearly with d until d=R.
2. Outside the Conductor: The magnetic field decreases inversely with d after d=R.
The correct representation of the magnetic field B as a function of distance d from the center of the cylindrical conductor is a graph that shows:
- A linear increase from the origin to d=R.
- A hyperbolic decrease for d>R.
Similar Questions
A circular coil of radius 2R is carrying current 'i' . The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionA cylindrical conductor of radius R carrying current i along the axis such that the magnetic field inside the conductor varies as B=B0r2(0<r≤R), then which of the following in incorrect?
View Solution
Knowledge Check
The correct plot of the magnitude of magnetic field →B vs distance r from centre of the wire is, if the radius of wire is R
A B
B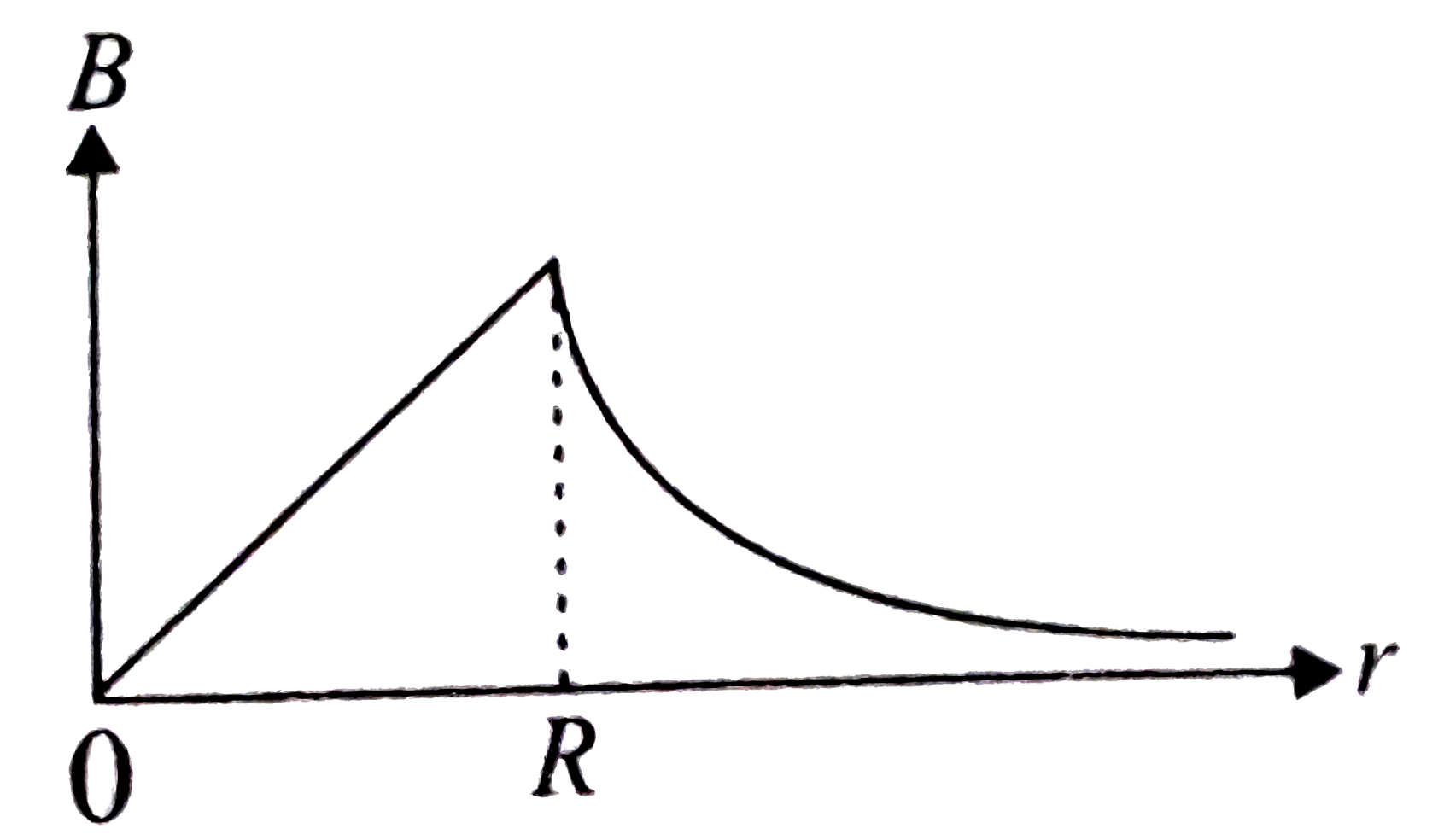 C
C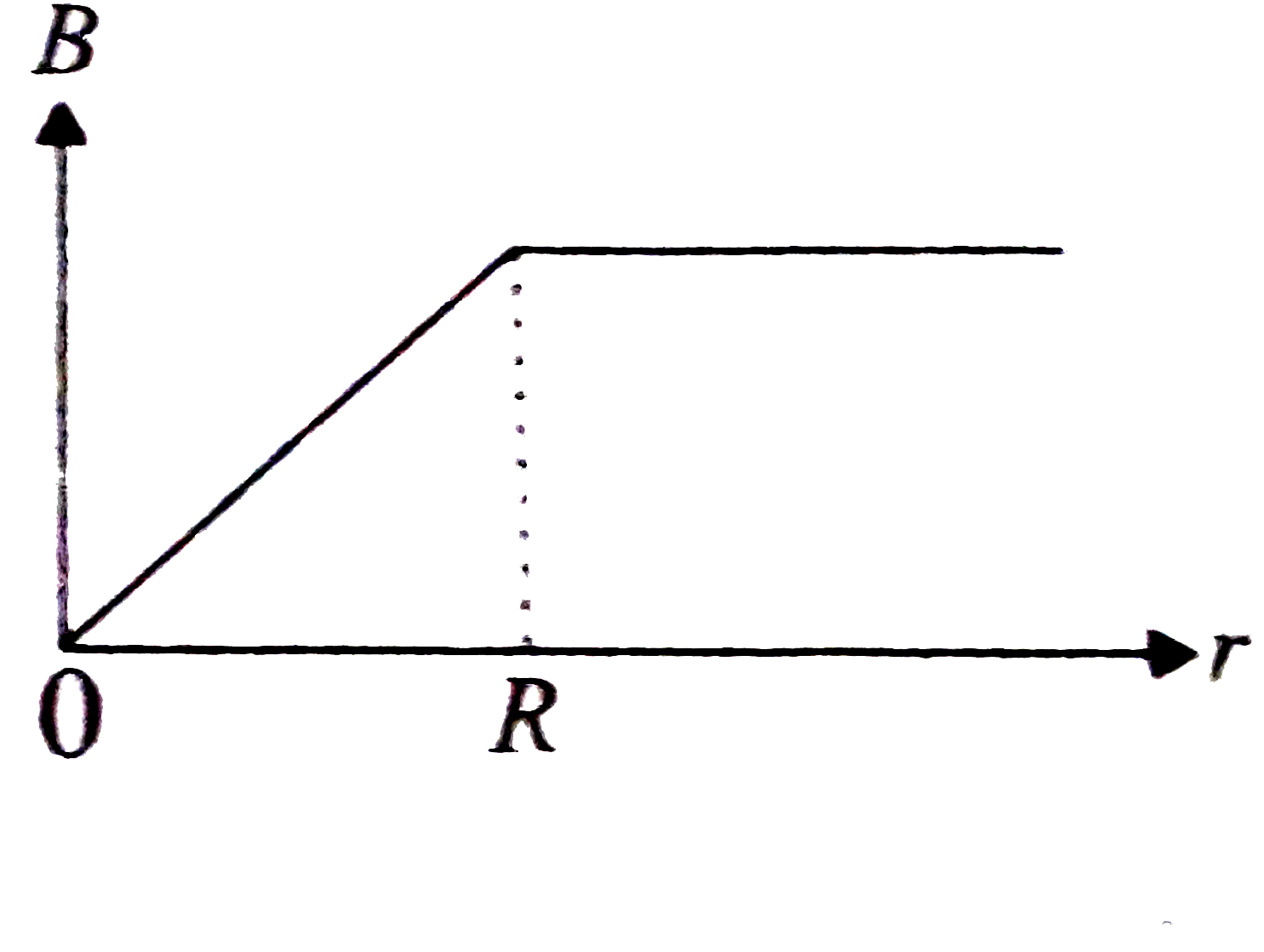 D
D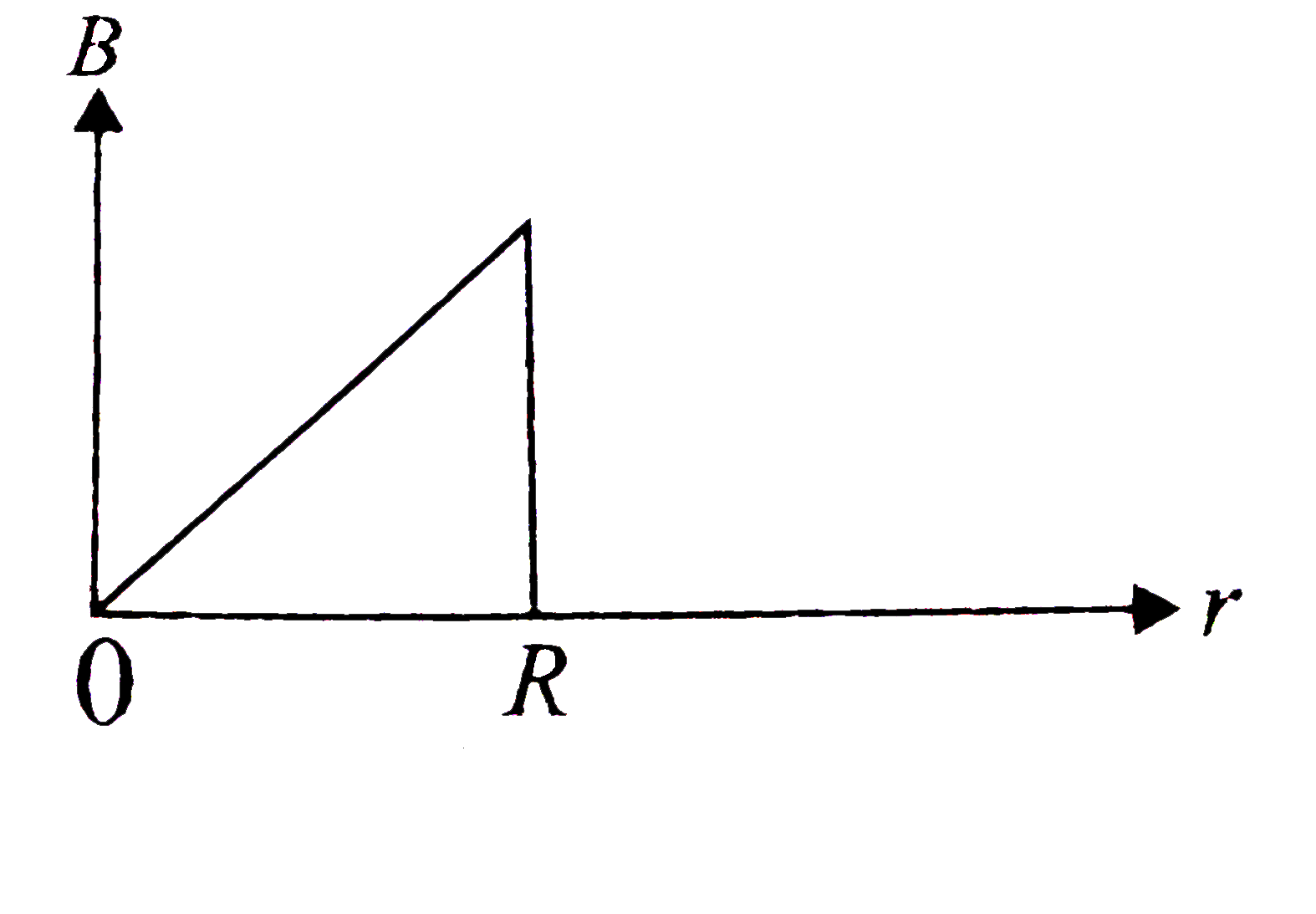
The magnitude of the magnetic field at the centre of the tightly wound 150 turn coil of radius 12 cm carrying a current of 2 A is
A18GB19.7GC15.7GD17.7G
A thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View SolutionAn infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA circular coil of radius R carries a current i. The magnetic field at its centre is B. The distance from the centre on the axis of the coil where the magnetic field will be B/8 is
View SolutionA cylindrical conductor of radius 'R' carries a current 'i'. The value of magnetic field at a point which is R/4 distance inside from the surface is 10T. Find the value of magnetic field at point which is 4R distance outside from the surface
View Solution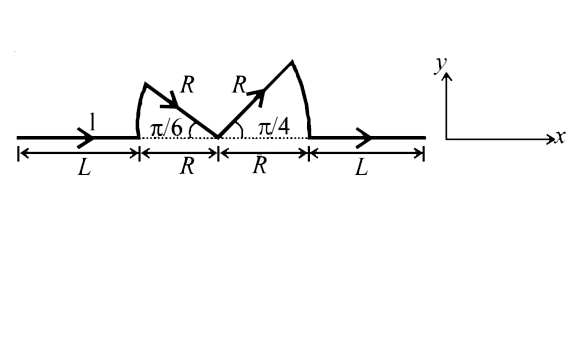
A conductor (shown in the figure) carrying constant current I is kept in the x-y plane in a uniform magnetic field B. If F is the magnitude of the total magnetic force acting on the conductor, then the correct statement is/are
View Solution