A cylindrical conductor of radius R carrying current i along the axis such that the magnetic field inside the conductor varies as B=B0r2(0<r≤R), then which of the following in incorrect?
Current density at distance 'r' from central axis of the conductor is J(r)=2B0rμ0
Current density at distance 'r' from central axis of the conductor is J(r)=3B0rμ0
Half of the total current would be confined within the radius of R(2)13 of the conductor
For r>R magnetic field would vary as B(r)=B0R3r
The correct Answer is:A
To solve the problem, we need to analyze the given magnetic field inside a cylindrical conductor and determine which of the provided statements is incorrect. The magnetic field inside the conductor is given by:
B=B0r2(0<r≤R)
where R is the radius of the cylindrical conductor and r is the distance from the central axis.
Step 1: Calculate the Current Density J
The current density J is defined as the current per unit area. We can find the current density using Ampère's law, which states:
μ0Ienc=∮B⋅dl
For a cylindrical conductor, the current enclosed Ienc at a radius r can be expressed as:
Ienc=J⋅A=J⋅πr2
Where A is the cross-sectional area of the cylinder at radius r.
Using Ampère's law, we can write:
μ0Ienc=B⋅(2πr)
Substituting B=B0r2:
μ0Ienc=(B0r2)⋅(2πr)=2πB0r3
Now, substituting for Ienc:
μ0J⋅πr2=2πB0r3
Dividing both sides by π:
μ0Jr2=2B0r3
Now, solving for J:
J=2B0r3μ0r2=2B0rμ0
Step 2: Analyze the Options
1. First Option: The current density at a distance r from the central axis is J=2B0rμ0. This is correct based on our calculation.
2. Second Option: We need to check if this option is incorrect. We will analyze the total current I0 flowing through the entire conductor.
Step 3: Total Current Calculation
Using Ampère's law for the entire conductor:
μ0I0=B0R2⋅(2πR)
Thus,
I0=B0R2⋅2πRμ0=2πB0R3μ0
Step 4: Half of the Total Current
To find the radius at which half of the total current I0/2 is enclosed, we set:
μ0I02=B0R20⋅(2πR0)
Substituting I0:
μ0⋅2πB0R3μ0⋅12=B0R20⋅(2πR0)
This simplifies to:
πB0R3=πB0R30
Thus, we find:
R30=R32
So,
R0=R⋅(12)1/3
Conclusion
After analyzing the options, we find that:
- The first option is correct.
- The second option is incorrect.
- The third option is also correct.
- The fourth option is correct.
Thus, the incorrect statement is the second option.
- The second option is incorrect.
- The third option is also correct.
- The fourth option is correct.
Similar Questions
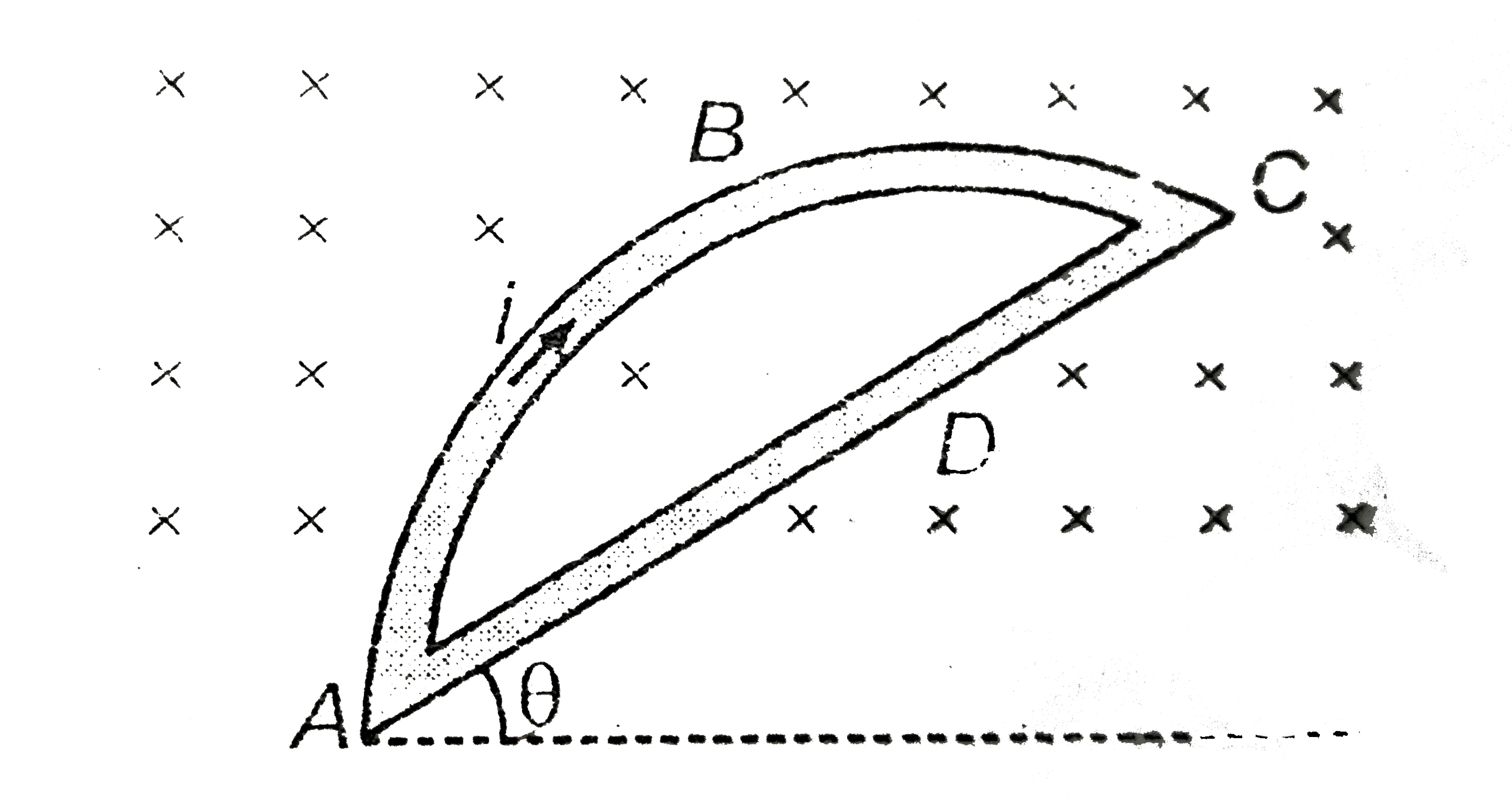
A circular wire ABC and a straight conductor ADC are carrying current i and are kept in the magnetic field B then
View SolutionA long copper tube of inner radius R carriers a current i. The magnetic field B inside the tube is
View SolutionA cylinderical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:
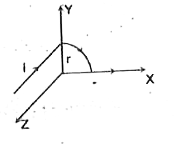
View SolutionShown in the figure is a conductor carrying a current i. the magnetic field at the origin is :
View SolutionA toroid with mean radius r0, diameter 2a have N turns carrying current l. What is the magnetic field B inside the the toroid?
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis

View SolutionA cylindrical conductor of radius 'R' carries a current 'i'. The value of magnetic field at a point which is R/4 distance inside from the surface is 10T. Find the value of magnetic field at point which is 4R distance outside from the surface
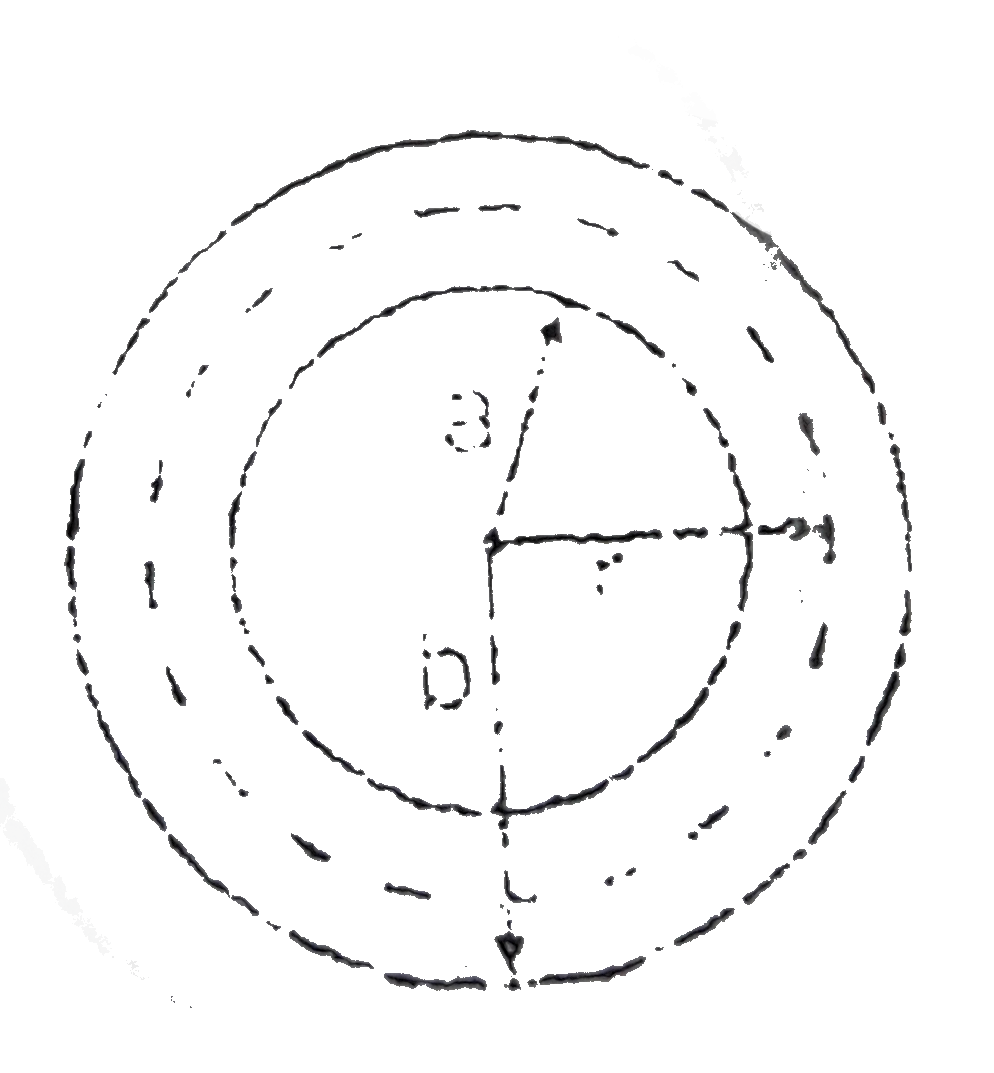
View SolutionFigure shows a cylindrical conductor of inner radius a & outer radius b which carries a current i unifromly spread over its cross section.Show that the magnetic field B for points inside the body of the conductor (i.e. a<r<b) is given by. B=μ0i2π(b2−a2)r2−a2r.Check this formula for the limiting case of a=0.
View SolutionA thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View SolutionA solid cylindrical conductor of radius R carries a current along its length.The current density J1 however, is not unifrom over the cross section of the conductor but is a function of the radius according to J=br, where b is a constant.the magnetic field B at r1<R is μ0br21N.Then find value of N
View Solution
