A thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
To solve the problem of finding the magnetic field due to a long hollow cylindrical tube carrying a current i, we will analyze two scenarios: (a) inside the tube and (b) outside the tube.
1. Identify the Distance from the Axis:
- The distance from the surface of the tube to the point of interest is r2.
- Therefore, the distance from the axis of the tube to the point inside is:
d=r−r2=r2
2. Apply Ampere's Circuital Law:
- According to Ampere's Circuital Law:
∮B⋅dl=μ0Iin
- Here, Iin is the current enclosed by the Amperian loop. Since the tube is hollow and the current flows only on the surface, there is no current enclosed inside the tube.
3. Conclusion for Inside the Tube:
- Since Iin=0:
∮B⋅dl=0⟹B=0
- Therefore, the magnetic field inside the tube at a distance r2 from the surface is:
Binside=0
(b) Magnetic Field Outside the Tube
1. Identify the Distance from the Axis:
- The distance from the surface of the tube to the point of interest is r2.
- Therefore, the distance from the axis of the tube to the point outside is:
d=r+r2=3r2
2. Apply Ampere's Circuital Law:
- For a point outside the tube, we can again use Ampere's Circuital Law:
∮B⋅dl=μ0Iin
- Here, Iin is the total current i flowing through the surface of the tube.
3. Set Up the Integral:
- The Amperian loop is a circle of radius x=3r2:
B⋅(2πx)=μ0i
- Substitute x=3r2:
B⋅(2π⋅3r2)=μ0i
4. Solve for Magnetic Field B:
- Simplifying gives:
B⋅3πr=μ0i⟹B=μ0i3πr
5. Conclusion for Outside the Tube:
- Therefore, the magnetic field outside the tube at a distance r2 from the surface is:
Boutside=μ0i3πr
Final Answers:
- (a) Inside the tube: Binside=0
- (b) Outside the tube: Boutside=μ0i3πr
- The distance from the surface of the tube to the point of interest is r2.
- Therefore, the distance from the axis of the tube to the point inside is:
d=r−r2=r2
- According to Ampere's Circuital Law:
∮B⋅dl=μ0Iin
- Here, Iin is the current enclosed by the Amperian loop. Since the tube is hollow and the current flows only on the surface, there is no current enclosed inside the tube.
- Since Iin=0:
∮B⋅dl=0⟹B=0
- Therefore, the magnetic field inside the tube at a distance r2 from the surface is:
Binside=0
- The distance from the surface of the tube to the point of interest is r2.
- Therefore, the distance from the axis of the tube to the point outside is:
d=r+r2=3r2
- For a point outside the tube, we can again use Ampere's Circuital Law:
∮B⋅dl=μ0Iin
- Here, Iin is the total current i flowing through the surface of the tube.
- The Amperian loop is a circle of radius x=3r2:
B⋅(2πx)=μ0i
- Substitute x=3r2:
B⋅(2π⋅3r2)=μ0i
- Simplifying gives:
B⋅3πr=μ0i⟹B=μ0i3πr
- Therefore, the magnetic field outside the tube at a distance r2 from the surface is:
Boutside=μ0i3πr
- (a) Inside the tube: Binside=0
- (b) Outside the tube: Boutside=μ0i3πr
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
A long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point (a) just inside the tube (b) just outside the tube.
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View Solution
Knowledge Check
The correct plot of the magnitude of magnetic field →B vs distance r from centre of the wire is, if the radius of wire is R
A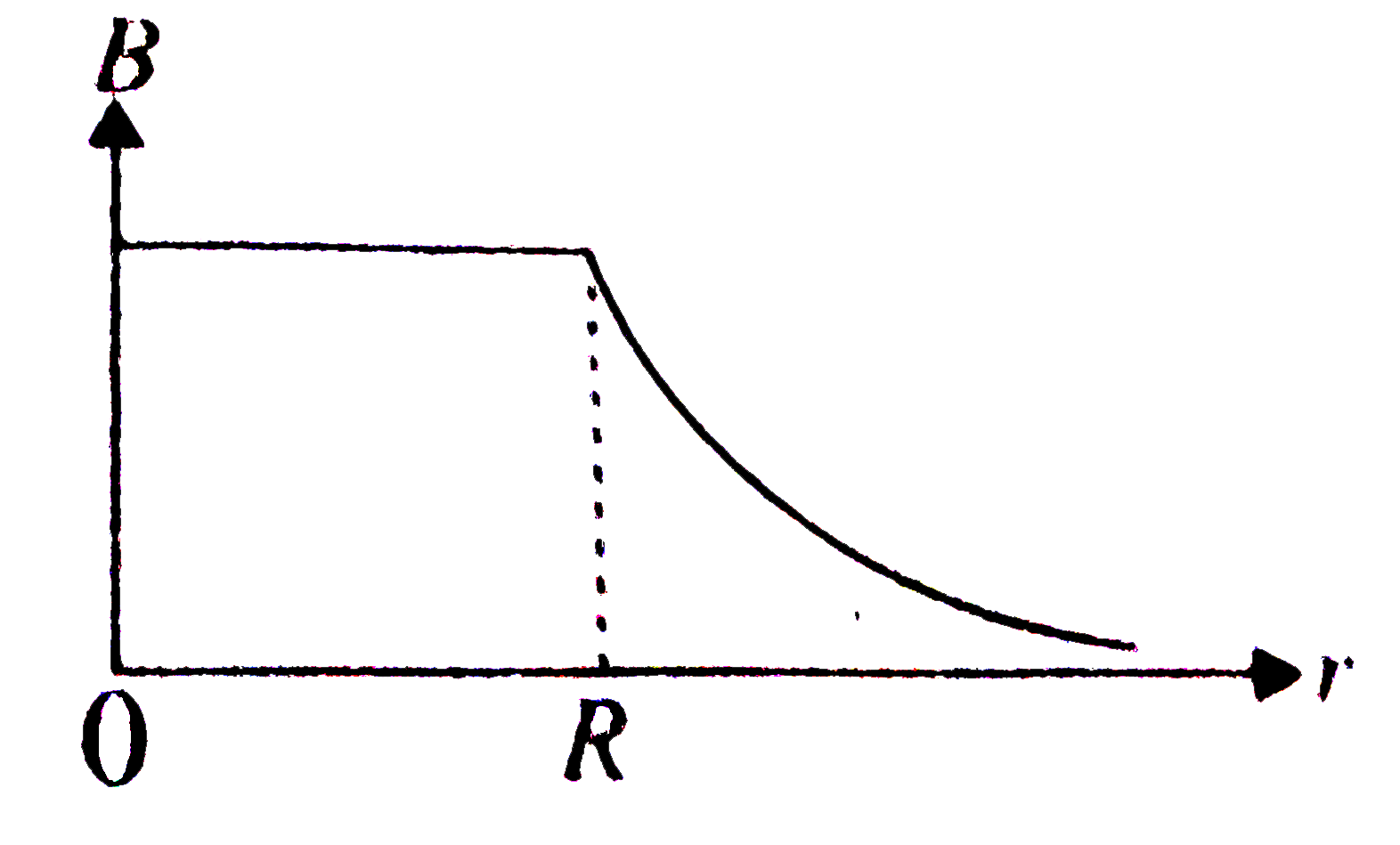 B
B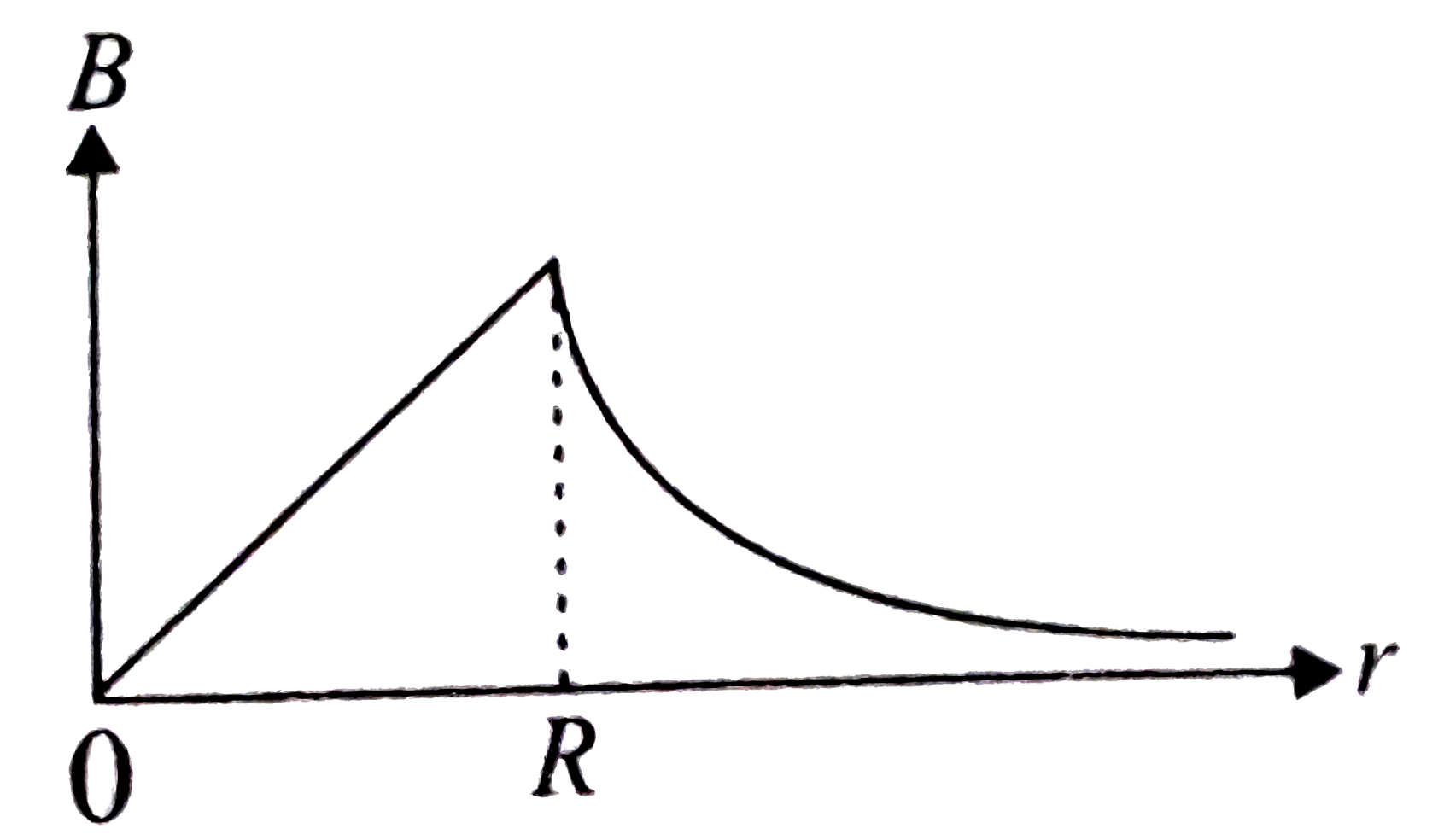 C
C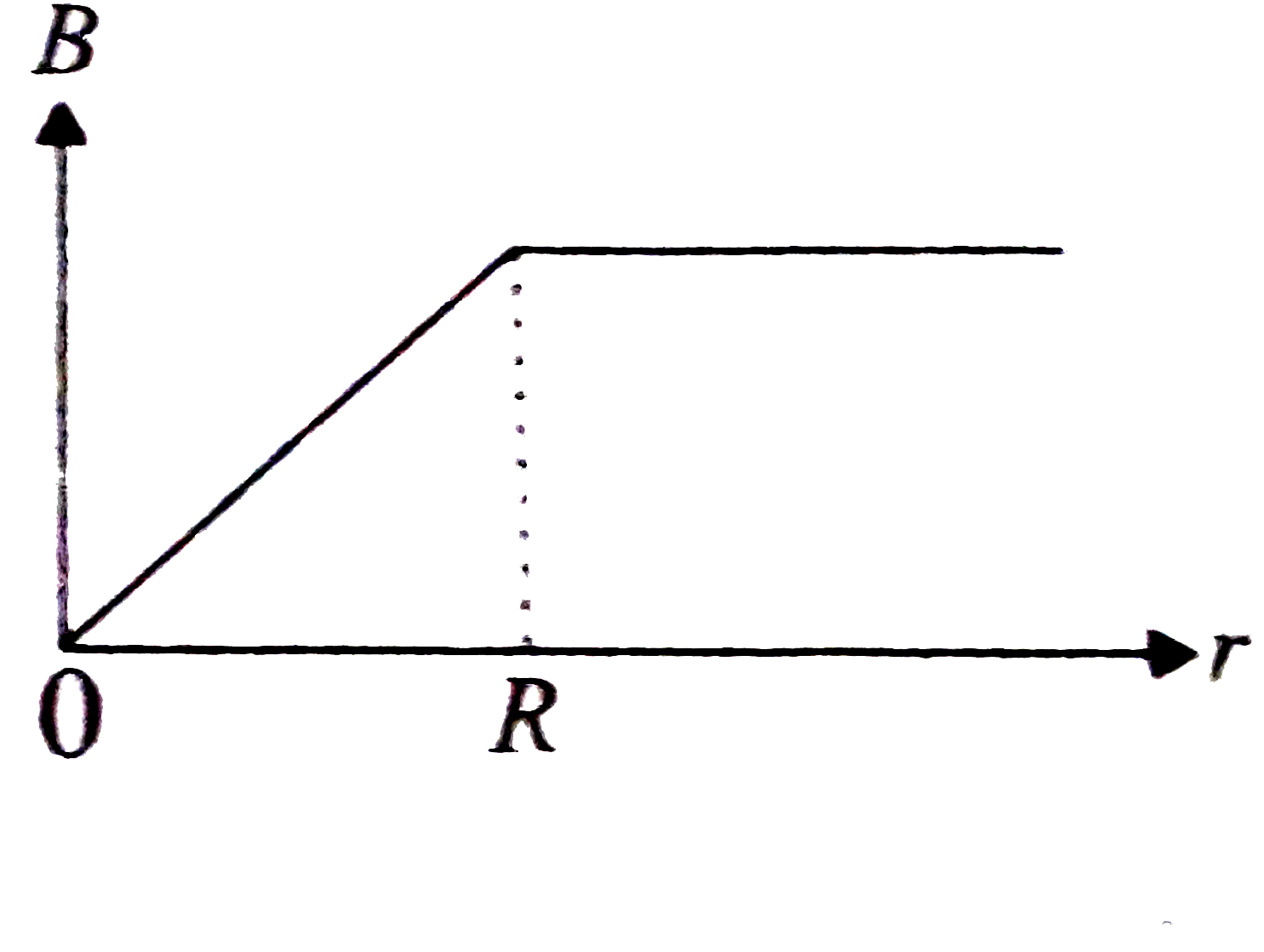 D
D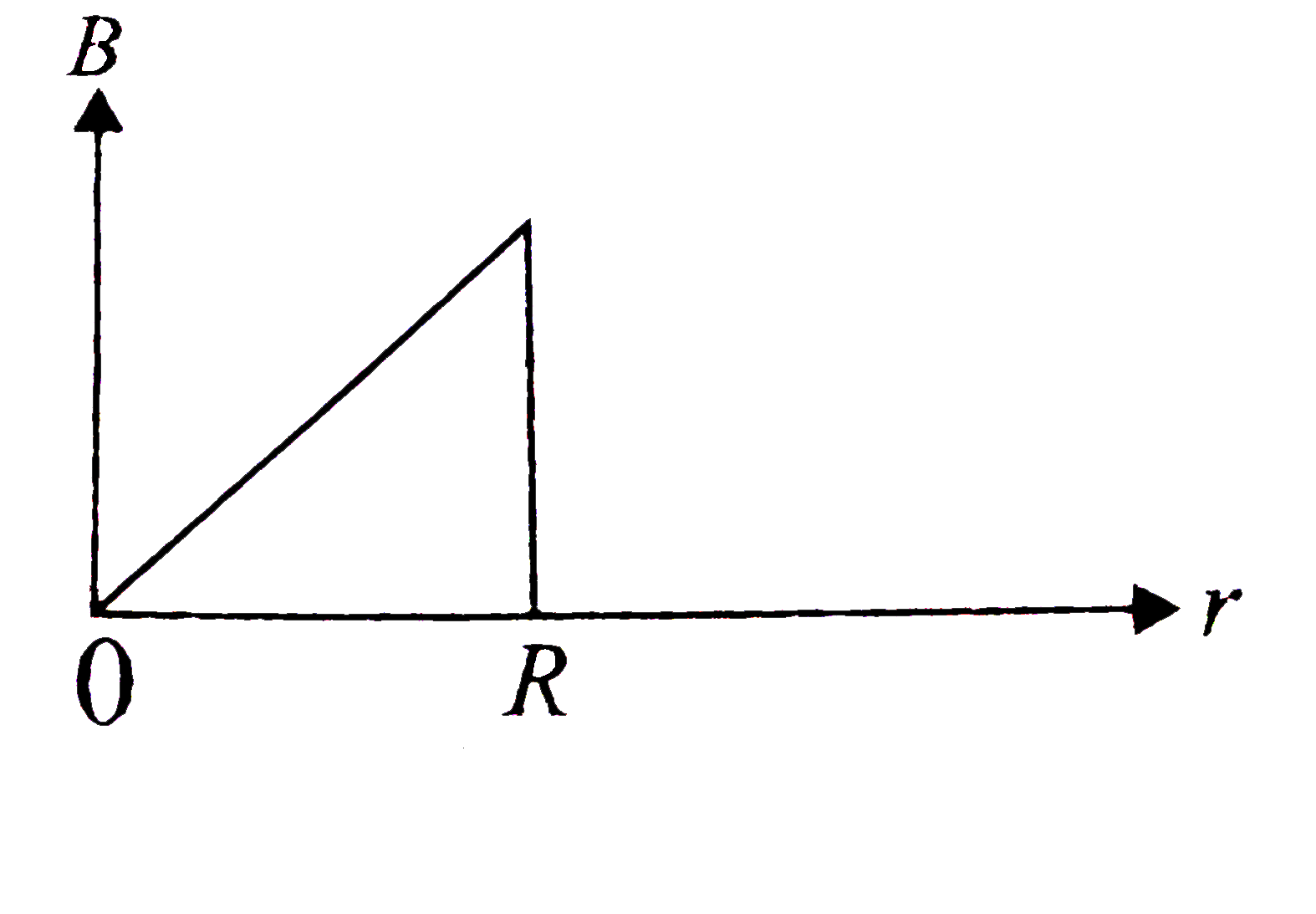
A long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
View SolutionA long, thick straight conductor of radius R carries current I uniformly distributed in its cross section area.The ratio of energy density of the magnetic field at distance R/2 from surface inside the conductor and outside the conductor is:
View SolutionA hollow tube is carrying an electric current along its length distributed uniformly over its surface. The magnetic field
View SolutionA long copper tube of inner radius R carriers a current i. The magnetic field B inside the tube is
View SolutionCurrent flows through a straight, thin-walled tube of radius r. The magnetic field at a distance x from the axis of the tube has magnitude B.
View SolutionAn infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
View Solution
