A particle starts its motion from rest under the action of a constant force. If the distance covered in first 10s is s1 and the covered in the first 20s is s2, then.
s2=2s1
s2=3s1
s2=4s1
s2=s1
The correct Answer is:C
To solve the problem step by step, we can use the equations of motion under constant acceleration. Here's the detailed solution:
Step 1: Understand the motion
The particle starts from rest under the influence of a constant force. This means that the initial velocity (u) is 0, and the particle experiences a constant acceleration (a).
Step 2: Write the equation for distance covered
The distance covered by an object under constant acceleration can be expressed using the equation:
s=ut+12at2
Since the particle starts from rest, u=0. Therefore, the equation simplifies to:
s=12at2
Step 3: Calculate distance for the first 10 seconds
Let the distance covered in the first 10 seconds be s1:
s1=12a(10)2
s1=12a⋅100
s1=50a (Equation 1)
Step 4: Calculate distance for the first 20 seconds
Now, let the distance covered in the first 20 seconds be s2:
s2=12a(20)2
s2=12a⋅400
s2=200a (Equation 2)
Step 5: Relate s1 and s2
Now, we can find the relationship between s1 and s2 by dividing Equation 1 by Equation 2:
s1s2=50a200a
The a cancels out:
s1s2=50200=14
Step 6: Express s2 in terms of s1
From the above relation, we can express s2 in terms of s1:
s2=4s1
Conclusion
Thus, the distance covered in the first 20 seconds is four times the distance covered in the first 10 seconds:
s2=4s1
The particle starts from rest under the influence of a constant force. This means that the initial velocity (u) is 0, and the particle experiences a constant acceleration (a).
The distance covered by an object under constant acceleration can be expressed using the equation:
s=ut+12at2
Since the particle starts from rest, u=0. Therefore, the equation simplifies to:
s=12at2
Let the distance covered in the first 10 seconds be s1:
s1=12a(10)2
s1=12a⋅100
s1=50a (Equation 1)
Now, let the distance covered in the first 20 seconds be s2:
s2=12a(20)2
s2=12a⋅400
s2=200a (Equation 2)
Now, we can find the relationship between s1 and s2 by dividing Equation 1 by Equation 2:
s1s2=50a200a
The a cancels out:
s1s2=50200=14
From the above relation, we can express s2 in terms of s1:
s2=4s1
Thus, the distance covered in the first 20 seconds is four times the distance covered in the first 10 seconds:
s2=4s1
Similar Questions
A particle start moving from rest state along a straight line under the action of a constant force and travel distance x in first 5 seconds. The distance travelled by it in next five seconds will be
View SolutionA bus starts from rest and moves whith acceleration a=2ms2. The ratio of the distance covered in 6th second to that covered in 6 seconds is
View SolutionAn object of mass 8 kg starts to move from rest under the action of a variable force F=3xN where x is the distance (in m) covered by the object. If initially, the position of the object is x = 2 m, then find its speed (in m s−1) when it crosses x = 10 m.
View SolutionA body starts from rest with a uniform acceleration of 2 m s−1 . Find the distance covered by the body in 2 s.
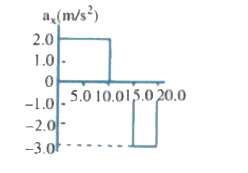
View SolutionA particle starts from rest and accelerates as shown in the graph .Determine (a)the particle's speed at t=10 s and t=20 s and (b)the distance travelled in the first 20 s.
View SolutionA body starts from rest and moves with constant acceleration. The ratio of distance covered by the body in nth second to that covered in n second is.
View SolutionA particle of mass 2 kg starts motion at time t = 0 under the action of variable force F = 4t (where F is in N and t is in s). The work done by this force in first two second is
View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.

View SolutionA particle starts from the rest, moves with constant acceleration for 15s. If it covers s1 distance in first 5s then distance s2 in next 10s, then find the relation between s1&s2.
View SolutionA particle experiences a constant acceleration for 20 sec after starting from rest. If it travels distance S1 in the first 10 sec and a distance S2 in the next 10 sec, Then
View Solution
