A particle of mass 2 kg starts motion at time t = 0 under the action of variable force F = 4t (where F is in N and t is in s). The work done by this force in first two second is
16 J
8 J
4 J
Zero
The correct Answer is:c
To solve the problem of finding the work done by a variable force on a particle of mass 2 kg over the first two seconds, we can follow these steps:
Step 1: Understand the Force
The force acting on the particle is given by the equation:
F(t)=4t
where F is in Newtons and t is in seconds.
Step 2: Calculate the Acceleration
Using Newton's second law, the acceleration a can be calculated as:
a=Fm
where m is the mass of the particle. Substituting the values:
a=4t2=2t
Step 3: Relate Acceleration to Velocity
We know that acceleration is the rate of change of velocity:
a=dvdt
Thus, we can write:
dvdt=2t
Step 4: Integrate to Find Velocity
To find the velocity v, we integrate both sides with respect to t:
∫dv=∫2tdt
This gives us:
v=t2+C
where C is the constant of integration. Since the particle starts from rest at t=0, we have:
v(0)=0⇒C=0
Thus, the velocity function is:
v(t)=t2
Step 5: Calculate the Velocity at t=2 seconds
Now, we can find the velocity at t=2 seconds:
v(2)=(2)2=4m/s
Step 6: Calculate the Change in Kinetic Energy
The work done by the force is equal to the change in kinetic energy. The kinetic energy KE is given by:
KE=12mv2
Calculating the initial kinetic energy at t=0:
KEinitial=12⋅2⋅02=0
Calculating the kinetic energy at t=2:
KEfinal=12⋅2⋅(4)2=12⋅2⋅16=16J
Step 7: Calculate the Work Done
The work done W is the change in kinetic energy:
W=KEfinal−KEinitial=16−0=16J
Final Answer
The work done by the force in the first two seconds is:
16J
---
The force acting on the particle is given by the equation:
F(t)=4t
where F is in Newtons and t is in seconds.
Using Newton's second law, the acceleration a can be calculated as:
a=Fm
where m is the mass of the particle. Substituting the values:
a=4t2=2t
We know that acceleration is the rate of change of velocity:
a=dvdt
Thus, we can write:
dvdt=2t
To find the velocity v, we integrate both sides with respect to t:
∫dv=∫2tdt
This gives us:
v=t2+C
where C is the constant of integration. Since the particle starts from rest at t=0, we have:
v(0)=0⇒C=0
Thus, the velocity function is:
v(t)=t2
Now, we can find the velocity at t=2 seconds:
v(2)=(2)2=4m/s
The work done by the force is equal to the change in kinetic energy. The kinetic energy KE is given by:
KE=12mv2
Calculating the initial kinetic energy at t=0:
KEinitial=12⋅2⋅02=0
Calculating the kinetic energy at t=2:
KEfinal=12⋅2⋅(4)2=12⋅2⋅16=16J
The work done W is the change in kinetic energy:
W=KEfinal−KEinitial=16−0=16J
The work done by the force in the first two seconds is:
16J
Topper's Solved these Questions
Similar Questions
Under the action of a force, a 2kg body moves such that its position x as a function of time is given by x=t33 where x is in meter and t in second. The work done by the force in the first two seconds is .
View SolutionUnder the action of a force, a 2kg body moves such that its position x as a function of time is given by x=t33 where x is in metre and t in second. The work done by the force in the first two seconds is .
View SolutionThe position x of a particle moving along x - axis at time (t) is given by the equation t=√x+2, where x is in metres and t in seconds. Find the work done by the force in first four seconds
View SolutionUnder the action of a force, a 1 kg body moves, such that its position x as function of time t is given by x=t32. where x is in meter and t is in second. The work done by the force in fiest 3 second is
View SolutionA particle of mass 2kg starts to move at position x=0 and time t=0 under the action of force F=(10+4x)N along the x− axis on a frictionless horizontal track . Find the power delivered by the force in watts at the instant the particle has moved by distance 5m.
View SolutionUnder the action of a force a 2 kg body moves such that its position x in meters as a function of time t is given by x=t44+3. Then work done by the force in first two seconds is
View SolutionThe distance x moved by a body of mass 0.5 kg under the action of a force varies with time t as
x(m)=3t2+4t+5
Here, t is expressed in second. What is the work done by the force in first 2 seconds?
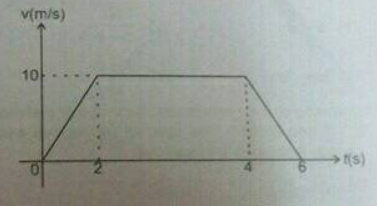
View SolutionA particle of mass 1 kg is moved under the action of a force and velocity time graph of the particle is shown in figure.Work done by the force from t=0 to t=6 s Is
View SolutionA force acts on a 3.0 gm particle in such a way that the position of the particle as a function of time is given by x=3t−4t2+t3, where xx is in metres and t is in seconds. The work done during the first 4 seconds is
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
View Solution
