An ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
Mg/k
2Mg/k
4Mg/k
Mg/2k
The correct Answer is:b
To solve the problem of finding the maximum extension in the spring when a block of mass M is attached and released, we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Understand the System
When the block is released, it will fall under the influence of gravity, and the spring will stretch as a result. Initially, the spring is unstretched, and the block has gravitational potential energy.
Step 2: Define the Variables
- Let k be the spring constant.
- Let M be the mass of the block.
- Let h be the maximum extension of the spring.
Step 3: Energy Conservation Principle
At the maximum extension h, the block momentarily comes to rest, meaning all its gravitational potential energy has been converted into spring potential energy.
The gravitational potential energy (P.E.) lost by the block as it falls a distance h is given by:
P.E.gravity=Mgh
The potential energy stored in the spring when it is stretched by h is given by:
P.E.spring=12kh2
Step 4: Set Up the Energy Conservation Equation
According to the conservation of energy:
P.E.gravity=P.E.spring
Substituting the expressions for potential energy:
Mgh=12kh2
Step 5: Rearrange the Equation
Rearranging the equation gives:
12kh2−Mgh=0
This is a quadratic equation in terms of h:
12kh2−Mgh=0
Step 6: Solve the Quadratic Equation
Factoring out h:
h(12kh−Mg)=0
This gives us two solutions: h=0 (the trivial solution) and:
12kh−Mg=0⟹kh=2Mg⟹h=2Mgk
Step 7: Conclusion
Thus, the maximum extension h in the spring is:
h=2Mgk
When the block is released, it will fall under the influence of gravity, and the spring will stretch as a result. Initially, the spring is unstretched, and the block has gravitational potential energy.
- Let k be the spring constant.
- Let M be the mass of the block.
- Let h be the maximum extension of the spring.
At the maximum extension h, the block momentarily comes to rest, meaning all its gravitational potential energy has been converted into spring potential energy.
P.E.gravity=Mgh
P.E.spring=12kh2
According to the conservation of energy:
P.E.gravity=P.E.spring
Substituting the expressions for potential energy:
Mgh=12kh2
Rearranging the equation gives:
12kh2−Mgh=0
This is a quadratic equation in terms of h:
12kh2−Mgh=0
Factoring out h:
h(12kh−Mg)=0
This gives us two solutions: h=0 (the trivial solution) and:
12kh−Mg=0⟹kh=2Mg⟹h=2Mgk
Thus, the maximum extension h in the spring is:
h=2Mgk
Similar Questions
A block of mass m attached in the lower and vertical spring The spring is hung from a calling and force constant value k The mass is released from rest with the spring initially unstreched The maximum value of extension produced in the length of the spring will be
View SolutionIn a vertical spring mass system, a block of mass m is initially at rest when there is no extension. Now if the mass is released suddenly, then the maximum elongation in the spring is
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass 2m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched. Find the maximum extension in the spring and acceleration of block B at time of maximum extension
 .
.
View SolutionFigure a) shows a spring of force constant k clamped rigidly at once end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?

View SolutionFigure a) shows a spring of force constant k clamped rigidly at once end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?

View SolutionConsider the situation shown in figure.
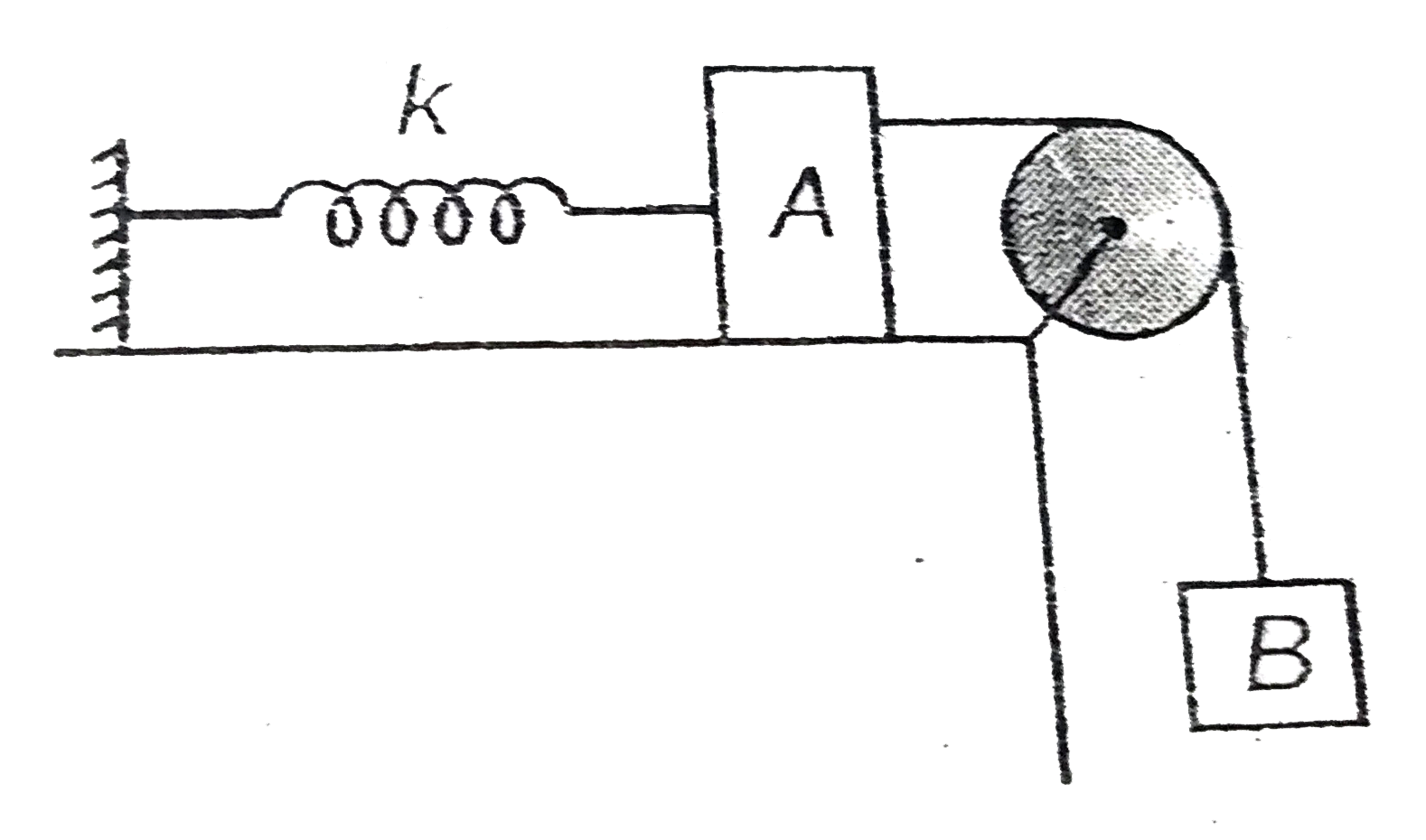
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.
View SolutionConsider the system shown below, with two equal masses m and a spring with spring constant K. The coefficient of friction between the left mass and horizontal table is μ=1/4, and the pulley is frictionless. The spring connecting both the blocks is massless and inelastic. The system is held with the spring at its unstretched length and then released.
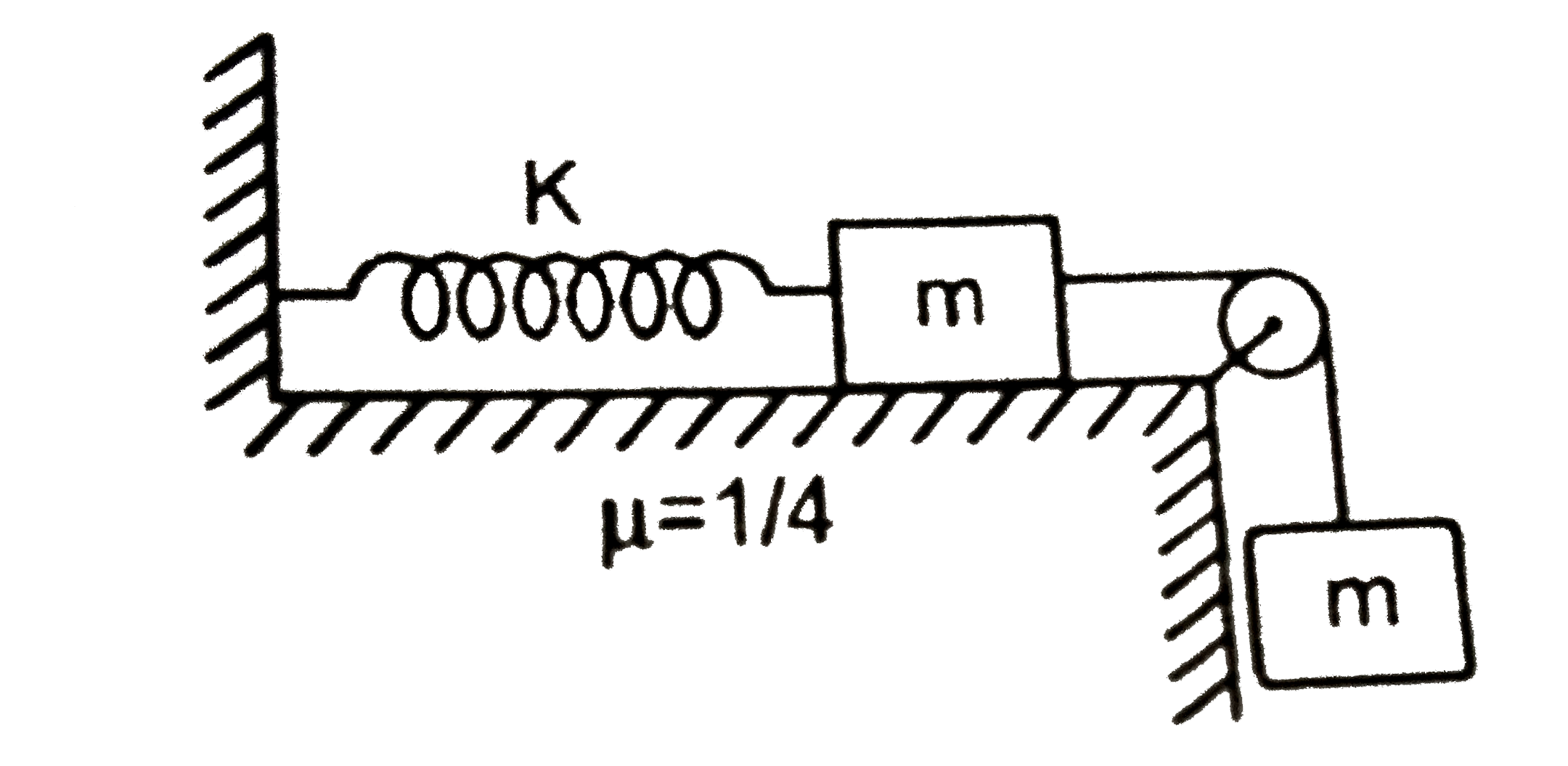
The extension in spring when the masses come to momentary rest for the first time is
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
