In the adjoining figure, block A is of mass (m) and block B is of mass 2m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched. Find the maximum extension in the spring and acceleration of block B at time of maximum extension
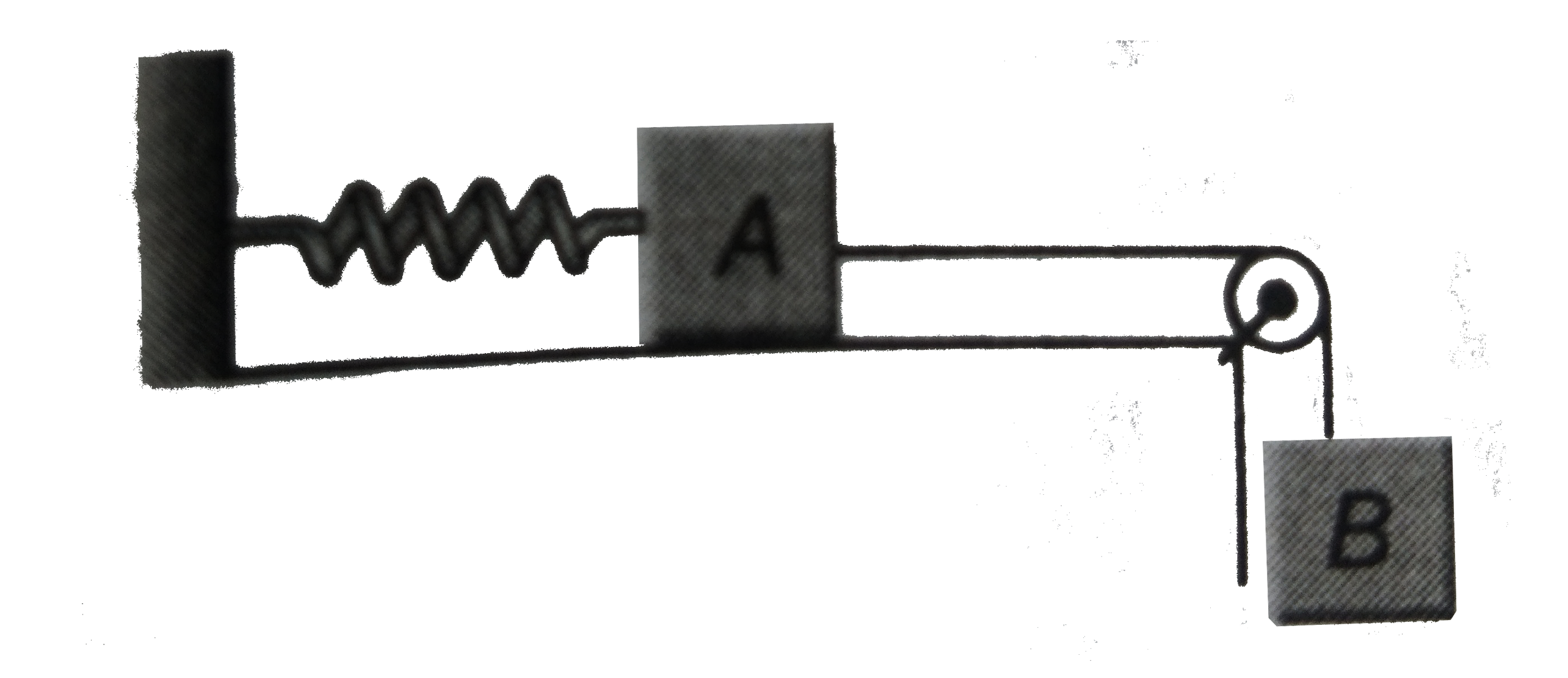 .
.
The correct Answer is:A, B, C, D
(a) At maximum extension in the spring
vA=vB=0 Therefore, appluing conservation of mechanical energy:
(momentarilt)
Therefore, appluing conservation of mechanical energy:
decreasing in gravitational energy of block B = incrasing in elastic potential
enerrgy of spring .
or mBgxM=12Kx2m
or 2mgxm=12Kx2m
:. xm=4mgK
(b) At x=xm2=2mgK
Let vA=vB=v(say)
The decrase in gravitational potential energy of block (B) =increase in elastic potential energy of spring + increase in kinetic inergy of both the blocks.
∴mBgx=12Kx2+12(mA+mB)v2
or (2m)(g)(2mgk)=12K(2mgK)2+12(m+2m)v2
∴v=2g√m2K
(c) At x=xm4=mgK
 .
.
or Kx=mg
a=Netpl–∈gforceTotalmass=2mg−mg3m
=g3(downwards).
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE21videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Miscellaneous Example6videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
In the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
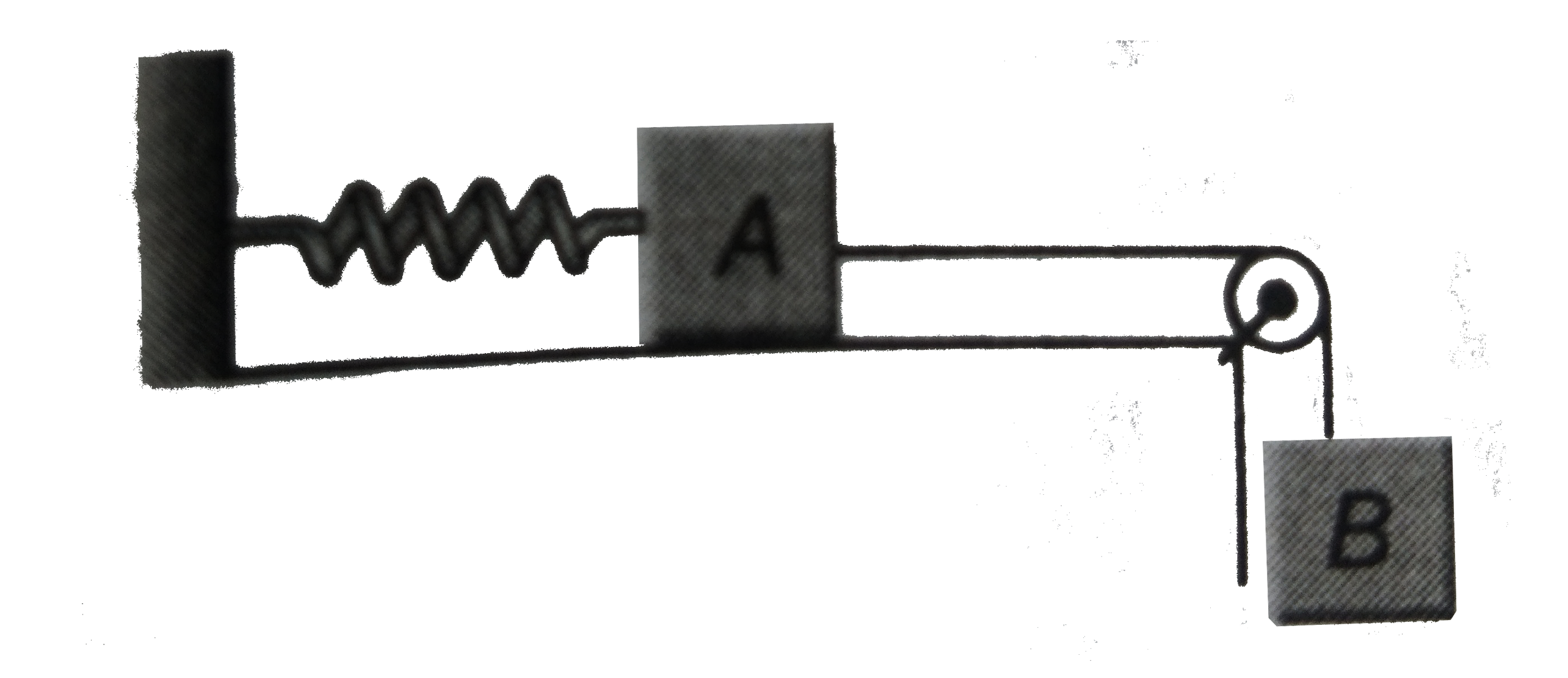 .View Solution
.View SolutionConsider the situation shown in figure.
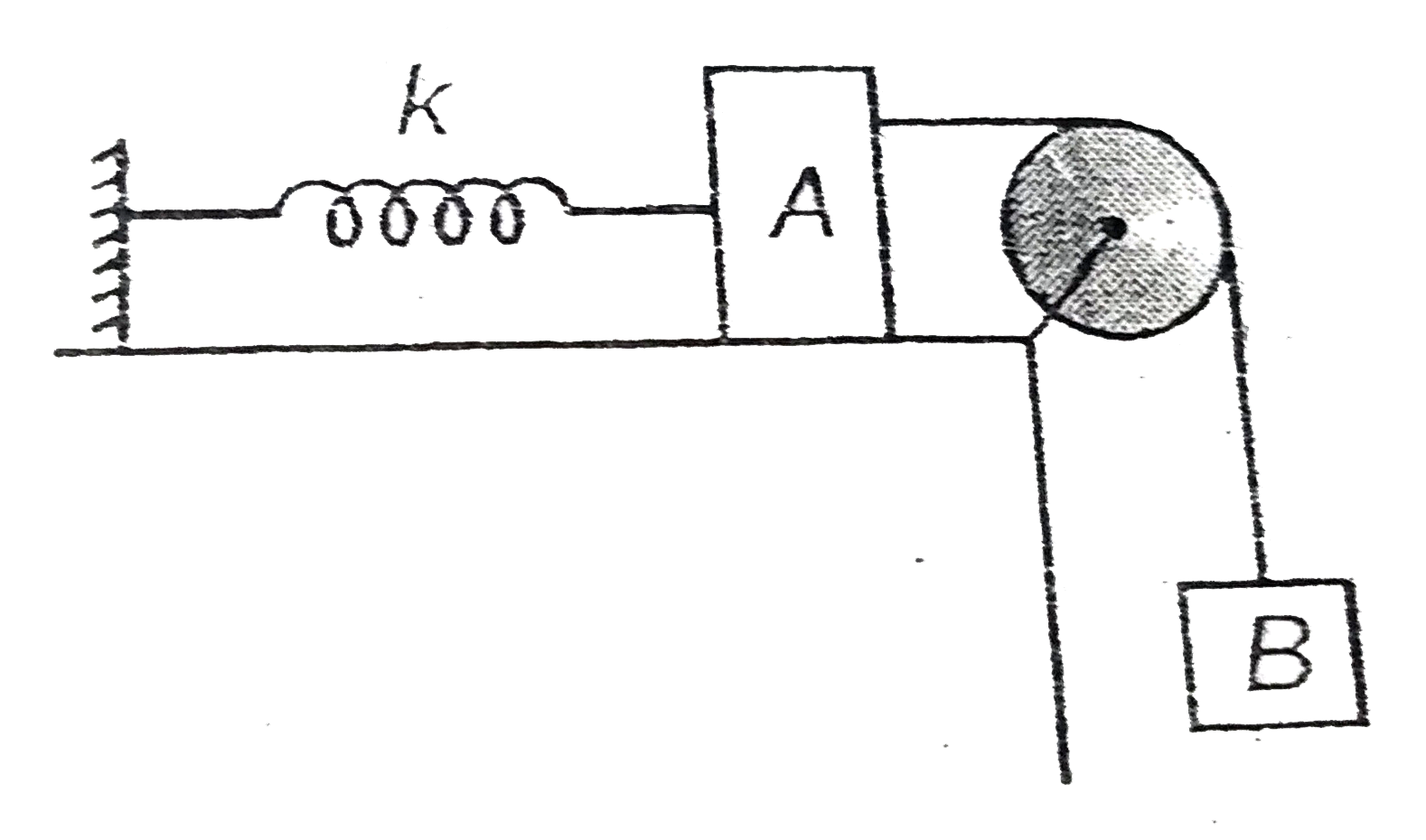
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
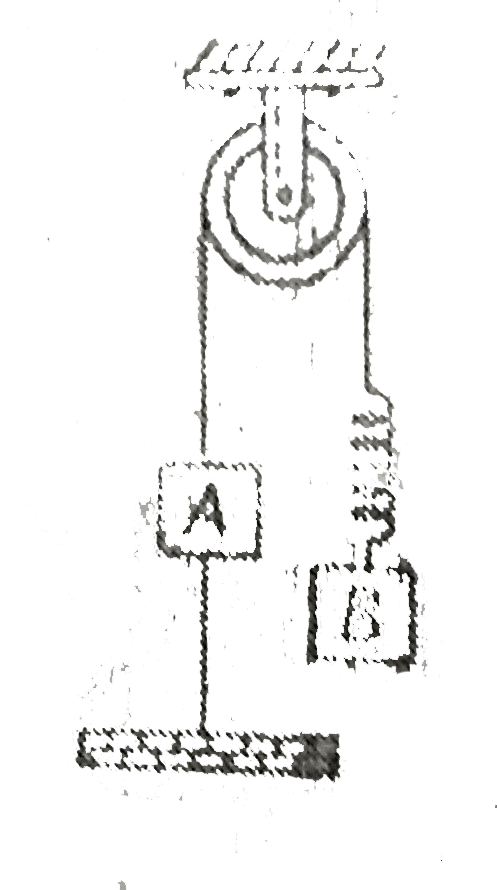 View Solution
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionA block of mass m attached in the lower and vertical spring The spring is hung from a calling and force constant value k The mass is released from rest with the spring initially unstreched The maximum value of extension produced in the length of the spring will be
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 View Solution
View SolutionA block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
View SolutionA block of mass m is suddenly released from the top of a spring of stiffness constant k.
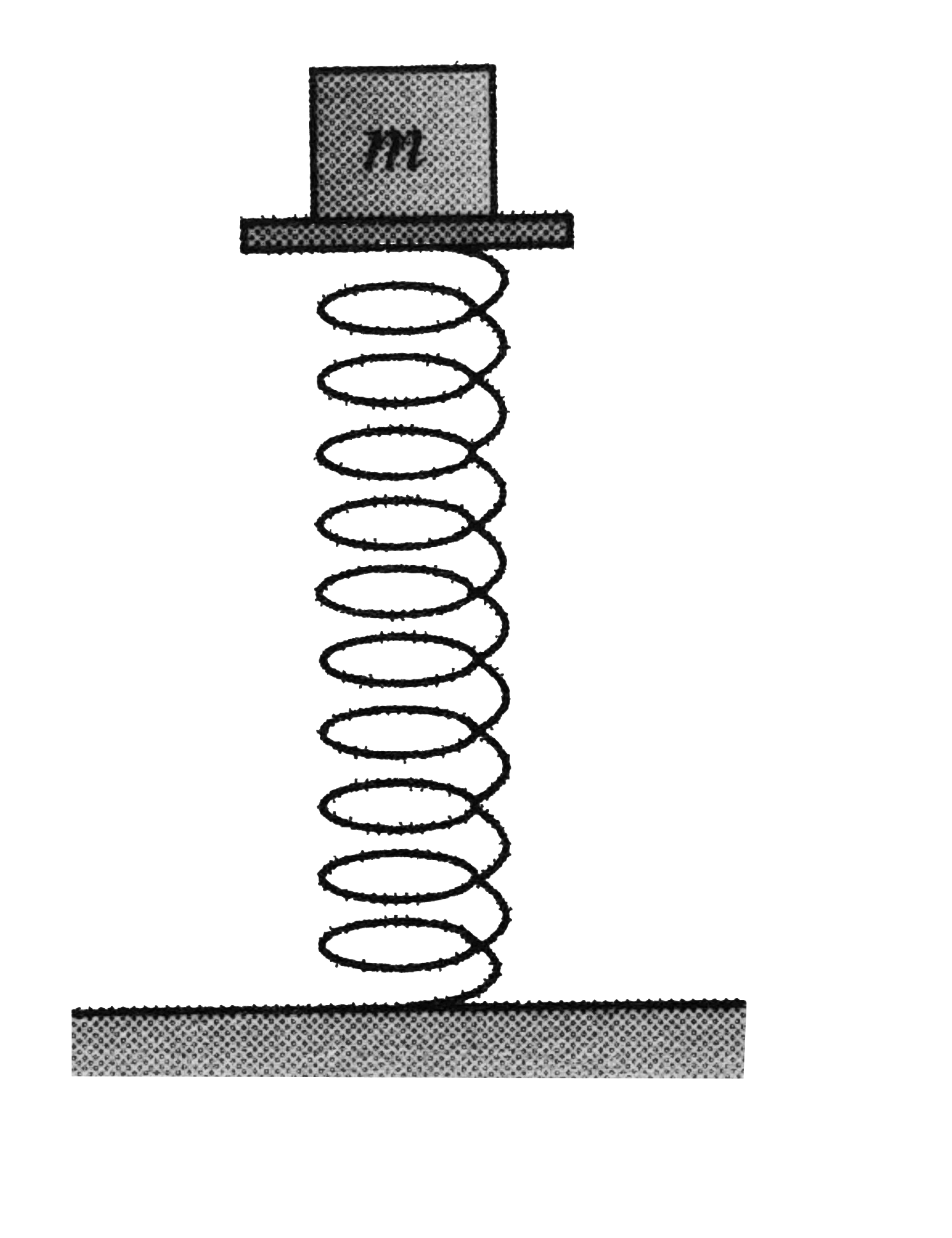
a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring
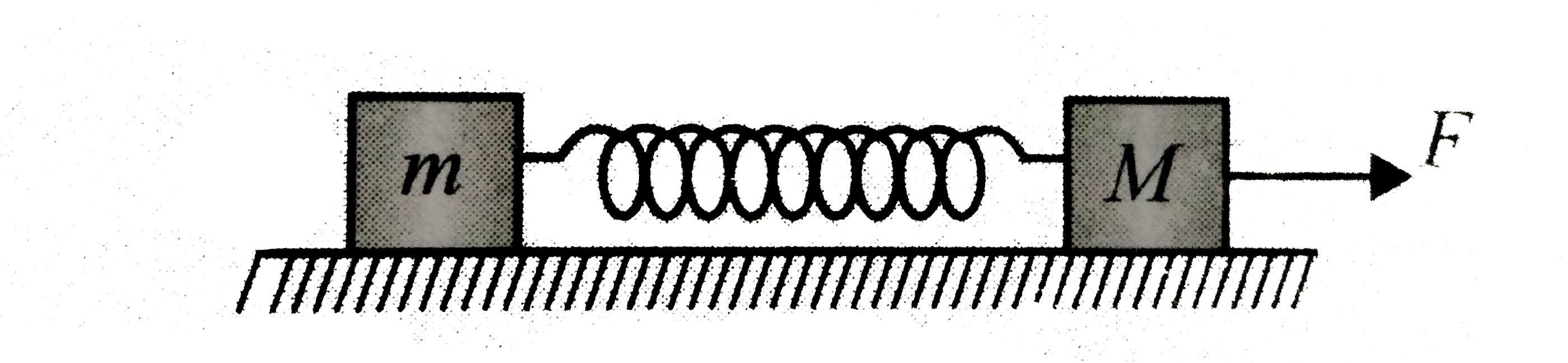 View Solution
View Solution

