A block of mass m attached in the lower and vertical spring The spring is hung from a calling and force constant value k The mass is released from rest with the spring initially unstreched The maximum value of extension produced in the length of the spring will be
2Mgk
4Mgk
Mg2k
Mgk
The correct Answer is:A
To solve the problem of finding the maximum extension produced in the length of a spring when a block of mass m is attached to it, we can use the work-energy theorem. Here’s a step-by-step solution:
Step 1: Understand the System
We have a vertical spring with a spring constant k and a mass m attached to its lower end. The spring is initially unstretched, and the mass is released from rest.
Step 2: Identify Key Points
When the mass is released, it will fall under the influence of gravity until it reaches the maximum extension of the spring. At this point, the velocity of the mass will be zero.
Step 3: Apply the Work-Energy Theorem
According to the work-energy theorem, the work done on the system is equal to the change in kinetic energy. Initially, the kinetic energy is zero because the mass is at rest.
The work done by the gravitational force when the mass falls a distance Lmax is:
Wgravity=mgh=mgLmax
where h is the distance fallen, which is equal to the maximum extension Lmax.
The work done by the spring force when it is stretched by Lmax is:
Wspring=−12kL2max
(The negative sign indicates that the spring force acts in the opposite direction to the displacement.)
Step 4: Set Up the Equation
At maximum extension, the total work done by the gravitational force equals the work done on the spring:
mgLmax=12kL2max
Step 5: Rearrange the Equation
Rearranging the equation gives:
12kL2max−mgLmax=0
Factoring out Lmax:
Lmax(12kLmax−mg)=0
This gives us two solutions:
1. Lmax=0 (the trivial solution)
2. 12kLmax−mg=0
Step 6: Solve for Maximum Extension
From the second equation:
12kLmax=mg
Lmax=2mgk
Conclusion
The maximum extension produced in the length of the spring is:
Lmax=2mgk
We have a vertical spring with a spring constant k and a mass m attached to its lower end. The spring is initially unstretched, and the mass is released from rest.
When the mass is released, it will fall under the influence of gravity until it reaches the maximum extension of the spring. At this point, the velocity of the mass will be zero.
According to the work-energy theorem, the work done on the system is equal to the change in kinetic energy. Initially, the kinetic energy is zero because the mass is at rest.
Wgravity=mgh=mgLmax
where h is the distance fallen, which is equal to the maximum extension Lmax.
Wspring=−12kL2max
(The negative sign indicates that the spring force acts in the opposite direction to the displacement.)
At maximum extension, the total work done by the gravitational force equals the work done on the spring:
mgLmax=12kL2max
Rearranging the equation gives:
12kL2max−mgLmax=0
Factoring out Lmax:
Lmax(12kLmax−mg)=0
This gives us two solutions:
1. Lmax=0 (the trivial solution)
2. 12kLmax−mg=0
From the second equation:
12kLmax=mg
Lmax=2mgk
The maximum extension produced in the length of the spring is:
Lmax=2mgk
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
35 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
An ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionA ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
View SolutionA block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass 2m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched. Find the maximum extension in the spring and acceleration of block B at time of maximum extension
 .
.
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionConsider the situation shown in figure.
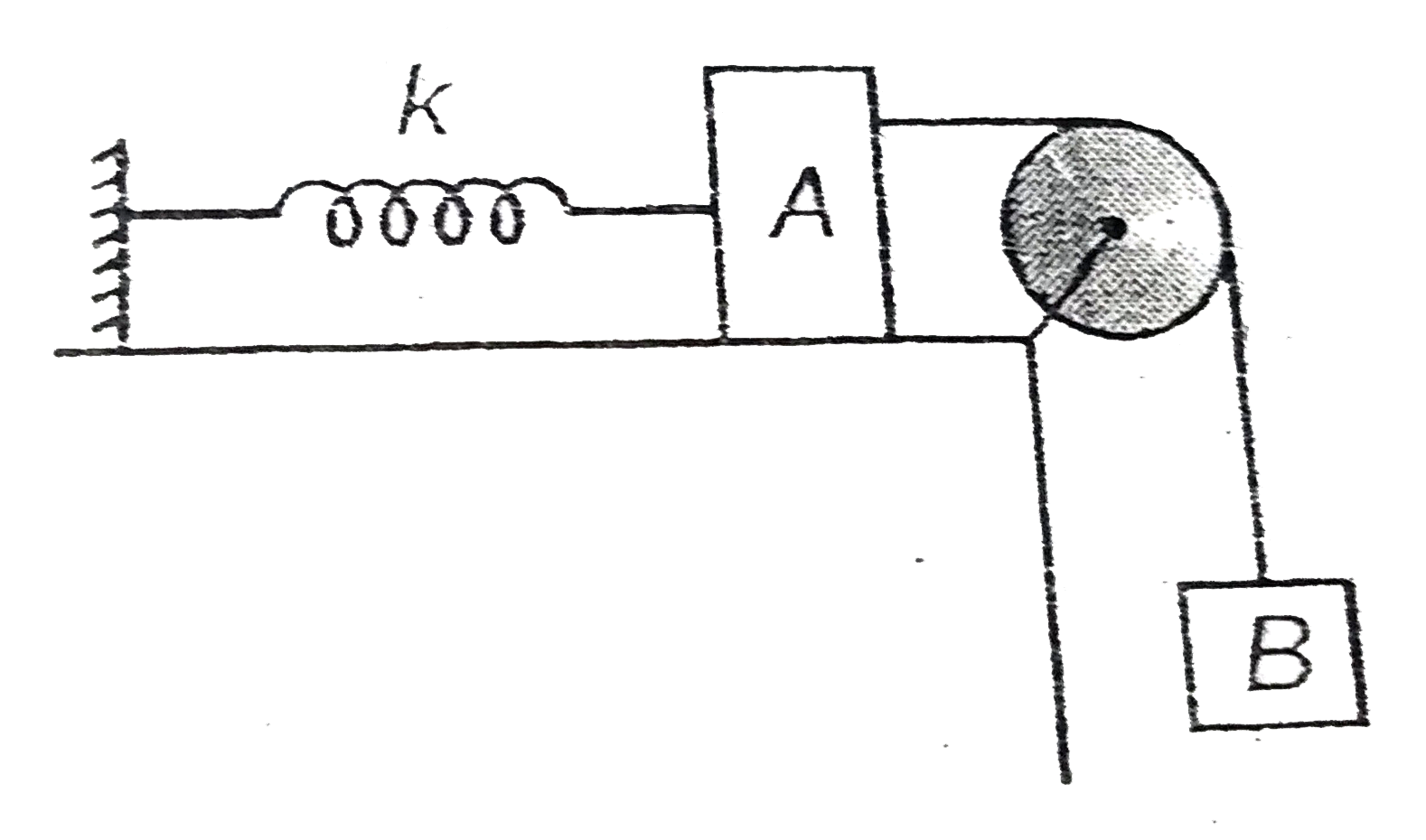
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.
View SolutionIn an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
 .
.
View Solution
