The cofficient of restitution e for a perfectly elastic collision is
(a) 1
(b) zero
(c) infinite
(d) -1
1
zero
infinite
-1
The correct Answer is:a
Step by step video & image solution for The cofficient of restitution e for a perfectly elastic collision is (a) 1 (b) zero (c) infinite (d) -1 by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The coefficient of restitution e for a perfectly elastic collision is
View SolutionA uniform rod of mass m and length L is hinged at one end and free to rotate in the horizontal plane. All the surface are smooth. A particle of same mass m collides with the rod with a speed V0. The coefficient of restitution for the collision is e=12. If hinge reaction during the collision is zero then the value of x is :

View SolutionFor perfectly inelastic collision cofficient of restitution e is
View Solution
Derive final velocities V1andV2 after perfectly elastic collision.
View SolutionA ball of mass 1kg is dropped from a height of 3.2m on smooth inclined plane. The coefficient of restitution for the collision is e=1/2. The ball's velocity become horizontal after the collision.

View SolutionMolecular collisions are perfectly elastic.
View SolutionThree identical block A, B and C are placed on a horizontal frictionless surface. The blocks B and C are at rest but A is approaching towards B with a speed 10ms−1. The coefficient of restitution for all collisions is 0.5. The speed of the block C just after the collision is

View SolutionThree identical blocks A, B and C are placed on horizontal frictionless surface. The blocks B and C are at rest. But A is approaching towards B with a speed of 10ms−1
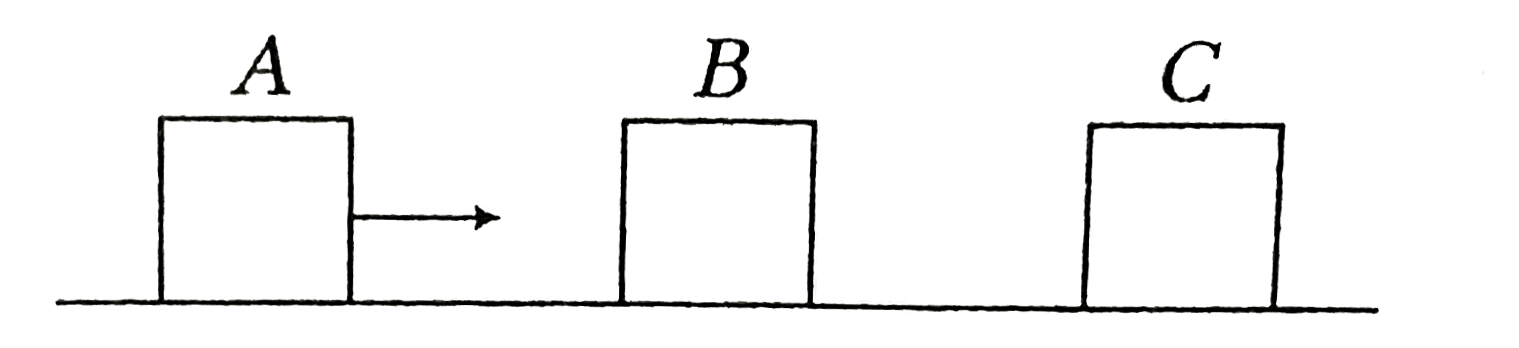
The coefficient of restitution for all collision is 0.5. The speed of the block C just after collision is
View SolutionStatement-1 : The coefficient of restitution is less than one for all collision studied under Newton's laws of restituation.
and
Statement-2 : For a perfeclty elastic collision, coefficient of restitution is equal to one .
View SolutionConsider objects of masses m1andm2 moving initially along the same straight line with velocities u1andu2 respectively. Considering a perfectly elastic collision (with u1>u2) derive expressions for their velocities after collision.
View Solution
