Question

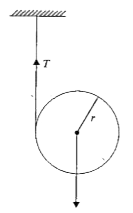
A solid cylinder of mass $50kg$ and radius $0.5m$ is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other end hanging freely. Tension in the string required to produce an angular acceleration of $2$ revolution $s^{-2}$ is

Options

A. `25 N`
B. `50 N`
C. `78.5 N`
D. `157 N`

Answer

d

Explanation

To solve the problem, we need to find the tension in the string that produces an angular acceleration of the solid cylinder. Here’s a step-by-step solution:

Step 1: Convert Angular Acceleration
The angular acceleration is given as \( 2 \, \text{revolutions/s}^2 \). We need to convert this to radians per second squared because the standard unit for angular acceleration in physics is radians.

\( \alpha = 2 \, \text{revolutions/s}^2 \times 2\pi \, \text{radians/revolution} = 4\pi \, \text{radians/s}^2 \)

Step 2: Calculate Moment of Inertia
The moment of inertia \( I \) for a solid cylinder rotating about its central axis is given by the formula:

\( I = \frac{1}{2} m r^2 \)

Where:
- \( m = 50 \, \text{kg} \) (mass of the cylinder)
- \( r = 0.5 \, \text{m} \) (radius of the cylinder)

Substituting the values:

\( I = \frac{1}{2} \times 50 \, \text{kg} \times (0.5 \, \text{m})^2 = \frac{1}{2} \times 50 \times 0.25 = 6.25 \, \text{kg m}^2 \)

Step 3: Relate Torque and Angular Acceleration
The torque \( \tau \) produced by the tension \( T \) in the string is given by:

\( \tau = T \times r \)

According to Newton's second law for rotation, the relationship between torque and angular acceleration is:

\( \tau = I \alpha \)

Step 4: Set Up the Equation
Equating the two expressions for torque:

\( T \times r = I \alpha \)

Substituting the known values:

\( T \times 0.5 = 6.25 \times 4\pi \)

Step 5: Solve for Tension
Now we can solve for \( T \):

\( T = \frac{6.25 \times 4\pi}{0.5} \)

Calculating the right side:

\( T = \frac{25\pi}{0.5} = 50\pi \)

Using \( \pi \approx 3.14 \):

\( T \approx 50 \times 3.14 = 157 \, \text{N} \)

Final Answer
The tension in the string required to produce the specified angular acceleration is approximately:

\( \boxed{157 \, \text{N}} \)

---